Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SSPR2, DSPR2, CHPR2, ZHPR2, SSYR2, DSYR2, CHER2, ZHER2, SSLR2, and DSLR2--Rank-Two Update of a Real Symmetric or Complex Hermitian Matrix

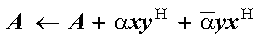
SSPR2, DSPR2, SSYR2, DSYR2, SSLR2, and DSLR2 compute the rank-two update of a real symmetric matrix, using the scalar alpha, matrix A, vectors x and y, and their transposes x^T and y^T:

A <-- A+alphaxy^T + alphayx^T

CHPR2, ZHPR2, CHER2, and ZHER2, compute the rank-two update of a complex Hermitian matrix, using the scalar alpha, matrix A, vectors x and y, and their conjugate transposes x^H and y^H:

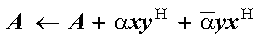
The following storage modes are used:

• For SSPR2, DSPR2, CHPR2, and ZHPR2, matrix A is stored in upper- or lower-packed storage mode.
• For SSYR2, DSYR2, CHER2, and ZHER2, matrix A is stored in upper or lower storage mode.
• For SSLR2 and DSLR2, matrix A is stored in lower-packed storage mode.

Table 66. Data Types

Note:

SSPR2 and DSPR2 are Level 2 BLAS subroutines. You should use these subroutines instead of SSLR2 and DSLR2, which are only provided for compatibility with earlier releases of ESSL.

Syntax

On Entry

uplo

indicates the storage mode used for matrix A, where:

If uplo = 'U', A is stored in upper-packed or upper storage mode.

If uplo = 'L', A is stored in lower-packed or lower storage mode.

Specified as: a single character. It must be 'U' or 'L'.

n

is the number of elements in vectors x and y and the order of matrix A. Specified as: a fullword integer; n >= 0.

alpha

is the scaling constant alpha. Specified as: a number of the data type indicated in Table 66.

x

is the vector x of length n. Specified as: a one-dimensional array of (at least) length 1+(n-1)|incx|, containing numbers of the data type indicated in Table 66.

incx

is the stride for vector x.

Specified as: a fullword integer, where:

For SSPR2, DSPR2, CHPR2, ZHPR2, SSYR2, DSYR2, CHER2, and ZHER2, incx < 0 or incx > 0.

For SSLR2 and DSLR2, incx can have any value.

y

is the vector y of length n. Specified as: a one-dimensional array of (at least) length 1+(n-1)|incy|, containing numbers of the data type indicated in Table 66.

incy

is the stride for vector y. Specified as: a fullword integer, where:

For SSPR2, DSPR2, CHPR2, ZHPR2, SSYR2, DSYR2, CHER2, and ZHER2, incy < 0 or incy > 0.

For SSLR2 and DSLR2, incy can have any value.

ap

has the following meaning:

For SSPR2 and DSPR2, ap is the real symmetric matrix A of order n, stored in upper- or lower-packed storage mode.

For CHPR2 and ZHPR2, ap is the complex Hermitian matrix A of order n, stored in upper- or lower-packed storage mode.

For SSLR2 and DSLR2, ap is the real symmetric matrix A of order n, stored in lower-packed storage mode.

Specified as: a one-dimensional array of (at least) length n(n+1)/2, containing numbers of the data type indicated in Table 66.

a

has the following meaning:

For SSYR2 and DSYR2, a is the real symmetric matrix A of order n, stored in upper or lower storage mode.

For CHER2 and ZHER2, a is the complex Hermitian matrix A of order n, stored in upper or lower storage mode.

Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 66.

lda

is the leading dimension of the array specified for a. Specified as: a fullword integer; lda > 0 and lda >= n.

On Return

ap

is the matrix A of order n, containing the results of the computation. Returned as: a one-dimensional array, containing numbers of the data type indicated in Table 66.

a

is the matrix A of order n, containing the results of the computation. Returned as: a two-dimensional array, containing numbers of the data type indicated in Table 66.

Notes

1. All subroutines accept lowercase letters for the uplo argument.
2. The vectors x and y must have no common elements with matrix A; otherwise, results are unpredictable. See Concepts.
3. On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <>  zero, the imaginary parts of the diagonal elements are set to zero.
4. For a description of how symmetric matrices are stored in upper- or lower-packed storage mode and upper or lower storage mode, see Symmetric Matrix. For a description of how complex Hermitian matrices are stored in upper- or lower-packed storage mode and upper or lower storage mode, see Complex Hermitian Matrix.

Function

These subroutines perform the computation described in the two sections below. See references [34], [35], and [79]. If n or alpha is zero, no computation is performed.

For SSPR2, SSYR2, SSLR2, CHPR2, and CHER2, intermediate results are accumulated in long precision.

SSPR2, DSPR2, SSYR2, DSYR2, SSLR2, and DSLR2

These subroutines compute the rank-two update of a real symmetric matrix:

A <-- A + alphaxy^T + alphayx^T

where:

A is a real symmetric matrix of order n.

alpha is a scalar.

x is a vector of length n.

x^T is the transpose of vector x.

y is a vector of length n.

y^T is the transpose of vector y.

It is expressed as follows:

CHPR2, ZHPR2, CHER2, and ZHER2

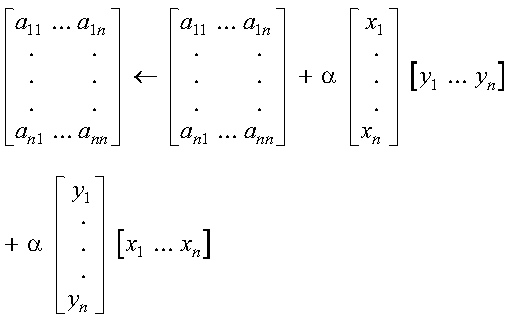
These subroutines compute the rank-two update of a complex Hermitian matrix:

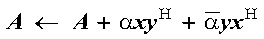
where:

A is a complex Hermitian matrix of order n.

alpha is a scalar.

x is a vector of length n.

x^H is the conjugate transpose of vector x.

y is a vector of length n.

y^H is the conjugate transpose of vector y.

It is expressed as follows:

Error Condition

Computational Errors

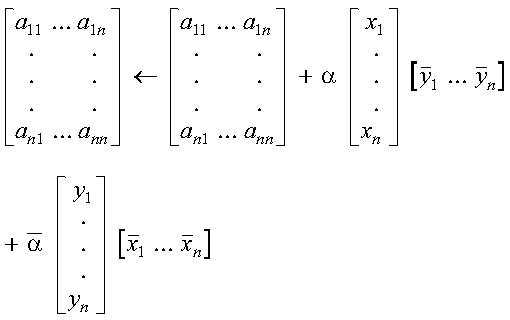
None

Input-Argument Errors

1. uplo <>  'L' or 'U'
2. n < 0
3. incx = 0
4. incy = 0
5. lda <= 0
6. lda < n

Example 1

This example shows vectors x and y with positive strides and a real symmetric matrix A of order 3, stored in lower-packed storage mode. Matrix A is:

                         *               *
                         | 8.0  4.0  2.0 |
                         | 4.0  6.0  7.0 |
                         | 2.0  7.0  3.0 |
                         *               *

Call Statement and Input

            UPLO  N  ALPHA  X  INCX  Y  INCY AP
             |    |    |    |   |    |   |   |
CALL SSPR2( 'L' , 3 , 1.0 , X , 1 ,  Y , 2 , AP )
 
X        =  (3.0, 2.0, 1.0)
Y        =  (5.0, . , 3.0, . , 2.0)
AP       =  (8.0, 4.0, 2.0, 6.0, 7.0, 3.0)

Output

AP       =  (38.0, 23.0, 13.0, 18.0, 14.0, 7.0)

Example 2

This example shows vector x and y having strides of opposite signs. For x, which has negative stride, processing begins at element X(5), which is 3.0. The real symmetric matrix A of order 3 is stored in upper-packed storage mode. It uses the same input matrix A as in Example 1.

Call Statement and Input

            UPLO  N  ALPHA  X   INCX Y  INCY AP
             |    |    |    |    |   |   |   |
CALL SSPR2( 'U' , 3 , 1.0 , X , -2 , Y , 2 , AP )
 
X        =  (1.0, . , 2.0, . , 3.0)
Y        =  (5.0, . , 3.0, . , 2.0)
AP       =  (8.0, 4.0, 6.0, 2.0, 7.0, 3.0)

Output

AP       =  (38.0, 23.0, 18.0, 13.0, 14.0, 7.0)

Example 3

This example shows vector x and y with positive stride and a complex Hermitian matrix A of order 3, stored in lower-packed storage mode. Matrix A is:

                    *                                      *
                    |  (1.0, 0.0)  (3.0, 5.0)  (2.0, -3.0) |
                    | (3.0, -5.0)  (7.0, 0.0)  (4.0, -8.0) |
                    |  (2.0, 3.0)  (4.0, 8.0)   (6.0, 0.0) |
                    *                                      *

Note:

On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <>  zero, the imaginary parts of the diagonal elements are set to zero.

Call Statement and Input

            UPLO  N   ALPHA   X  INCX Y  INCY AP
             |    |     |     |   |   |   |   |
CALL CHPR2( 'L' , 3 , ALPHA , X , 1 , Y , 2 , AP )
 
ALPHA    =  (1.0, 0.0)
X        =  ((1.0, 2.0), (4.0, 0.0), (3.0, 4.0))
Y        =  ((1.0, 0.0), . , (2.0, -1.0), . , (2.0, 1.0))
AP       =  ((1.0, . ), (3.0, -5.0), (2.0, 3.0), (7.0, . ),
             (4.0, 8.0), (6.0, . ))

Output

AP       =  ((3.0, 0.0), (7.0, -10.0), (9.0, 4.0), (23.0, 0.0),
             (14.0, 23.0), (26.0, 0.0))

Example 4

This example shows vector x and y having strides of opposite signs. For x, which has negative stride, processing begins at element X(5), which is (1.0,2.0). The complex Hermitian matrix A of order 3 is stored in upper-packed storage mode. It uses the same input matrix A as in Example 3.

Note:

On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <>  zero, the imaginary parts of the diagonal elements are set to zero.

Call Statement and Input

            UPLO  N   ALPHA   X  INCX  Y  INCY AP
             |    |     |     |    |   |   |   |
CALL CHPR2( 'U' , 3 , ALPHA , X , -2 , Y , 2 , AP )
 
ALPHA    =  (1.0, 0.0)
X        =  ((3.0, 4.0), . , (4.0, 0.0), . , (1.0, 2.0))
Y        =  ((1.0, 0.0), . , (2.0, -1.0), . , (2.0, 1.0))
AP       =  ((1.0, . ), (3.0, 5.0), (7.0, . ), (2.0, -3.0),
             (4.0, -8.0), (6.0, . ))

Output

AP       =  ((3.0, 0.0), (7.0, 10.0), (23.0, 0.0), (9.0, -4.0),
             (14.0, -23.0), (26.0, 0.0))

Example 5

This example shows vectors x and y with positive strides, and a real symmetric matrix A of order 3, stored in lower storage mode. It uses the same input matrix A as in Example 1.

Call Statement and Input

            UPLO  N  ALPHA  X  INCX Y  INCY A  LDA
             |    |    |    |   |   |   |   |   |
CALL SSYR2( 'L' , 3 , 1.0 , X , 1 , Y , 2 , A , 3 )
 
X        =  (3.0, 2.0, 1.0)
Y        =  (5.0, . , 3.0, . , 2.0)
 
        *               *
        | 8.0   .    .  |
A    =  | 4.0  6.0   .  |
        | 2.0  7.0  3.0 |
        *               *

Output

        *                 *
        | 38.0    .    .  |
A    =  | 23.0  18.0   .  |
        | 13.0  14.0  7.0 |
        *                 *

Example 6

This example shows vector x and y having strides of opposite signs. For x, which has negative stride, processing begins at element X(5), which is 3.0. The real symmetric matrix A of order 3 is stored in upper storage mode. It uses the same input matrix A as in Example 1.

Call Statement and Input

            UPLO  N  ALPHA  X  INCX  Y  INCY A  LDA
             |    |    |    |    |   |   |   |   |
CALL SSYR2( 'U' , 3 , 1.0 , X , -2 , Y , 2 , A , 4 )
 
X        =  (1.0, . , 2.0, . , 3.0)
Y        =  (5.0, . , 3.0, . , 2.0)
 
        *               *
        | 8.0  4.0  2.0 |
A    =  |  .   6.0  7.0 |
        |  .    .   3.0 |
        |  .    .    .  |
        *               *

Output

        *                  *
        | 38.0  23.0  13.0 |
A    =  |   .   18.0  14.0 |
        |   .     .    7.0 |
        |   .     .     .  |
        *                  *

Example 7

This example shows vector x and y with positive stride, and a complex Hermitian matrix A of order 3, stored in lower storage mode. It uses the same input matrix A as in Example 3.

Note:

On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <>  zero, the imaginary parts of the diagonal elements are set to zero.

Call Statement and Input

            UPLO  N   ALPHA   X  INCX Y  INCY A  LDA
             |    |     |     |   |   |   |   |   |
CALL CHER2( 'L' , 3 , ALPHA , X , 1 , Y , 2 , A , 3 )
 
ALPHA    =  (1.0, 0.0)
X        =  ((1.0, 2.0), (4.0, 0.0), (3.0, 4.0))
Y        =  ((1.0, 0.0), . , (2.0, -1.0), . , (2.0, 1.0))

        *                                    *
        |   (1.0, . )       .          .     |
A    =  | (3.0, -5.0)   (7.0, . )      .     |
        |  (2.0, 3.0)  (4.0, 8.0)  (6.0, . ) |
        *                                    *

Output

        *                                          *
        |   (3.0, 0.0)       .             .       |
A    =  | (7.0, -10.0)  (23.0, 0.0 )       .       |
        |   (9.0, 4.0)  (14.0, 23.0)  (26.0, 0.0 ) |
        *                                          *

Example 8

This example shows vector x and y having strides of opposite signs. For x, which has negative stride, processing begins at element X(5), which is (1.0, 2.0). The complex Hermitian matrix A of order 3 is stored in upper storage mode. It uses the same input matrix A as in Example 3.

Note:

On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <>  zero, the imaginary parts of the diagonal elements are set to zero.

Call Statement and Input

            UPLO  N   ALPHA   X  INCX  Y  INCY A  LDA
             |    |     |     |    |   |   |   |   |
CALL CHER2( 'U' , 3 , ALPHA , X , -2 , Y , 2 , A , 3 )
 
ALPHA    =  (1.0, 0.0)
X        =  ((3.0, 4.0), . , (4.0, 0.0), . , (1.0, 2.0))
Y        =  ((1.0, 0.0), . , (2.0, -1.0), . , (2.0, 1.0))

        *                                    *
        | (1.0, . ) (3.0, 5.0)   (2.0, -3.0) |
A    =  |     .      (7.0, . )   (4.0, -8.0) |
        |     .          .         (6.0, . ) |
        *                                    *

Output

        *                                        *
        | (3.0, 0.0)  (7.0, 10.0)    (9.0, -4.0) |
A    =  |     .       (23.0, 0.0)  (14.0, -23.0) |
        |     .            .         (26.0, 0.0) |
        *                                        *

Example 9

This example shows vectors x and y with positive strides and a real symmetric matrix A of order 3, stored in lower-packed storage mode. It uses the same input matrix A as in Example 1.

Call Statement and Input

            N  ALPHA  X  INCX  Y  INCY  AP
            |    |    |   |    |   |    |
CALL SSLR2( 3 , 1.0 , X , 1  , Y , 2  , AP )
 
X        =  (3.0, 2.0, 1.0)
Y        =  (5.0, . , 3.0, . , 2.0)
AP       =  (8.0, 4.0, 2.0, 6.0, 7.0, 3.0)

Output

AP       =  (38.0, 23.0, 13.0, 18.0, 14.0, 7.0)