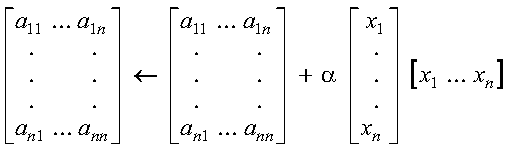

SSPR, DSPR, SSYR, DSYR, SSLR1, and DSLR1 compute the rank-one update of a real symmetric matrix, using the scalar alpha, matrix A, vector x, and its transpose xT:
CHPR, ZHPR, CHER, and ZHER compute the rank-one update of a complex Hermitian matrix, using the scalar alpha, matrix A, vector x, and its conjugate transpose xH:
The following storage modes are used:
| A, x | alpha | Subprogram |
| Short-precision real | Short-precision real | SSPR, SSYR, and SSLR1 |
| Long-precision real | Long-precision real | DSPR, DSYR, and DSLR1 |
| Short-precision complex | Short-precision real | CHPR and CHER |
| Long-precision complex | Long-precision real | ZHPR and ZHER |
| Fortran | CALL SSPR | DSPR | CHPR | ZHPR (uplo, n,
alpha, x, incx, ap)
CALL SSYR | DSYR | CHER | ZHER (uplo, n, alpha, x, incx, a, lda) CALL SSLR1 | DSLR1 (n, alpha, x, incx, ap) |
| C and C++ | sspr | dspr | chpr | zhpr (uplo, n, alpha,
x, incx, ap);
ssyr | dsyr | cher | zher (uplo, n, alpha, x, incx, a, lda); sslr1 | dslr1 (n, alpha, x, incx, ap); |
| PL/I | CALL SSPR | DSPR | CHPR | ZHPR (uplo, n,
alpha, x, incx, ap);
CALL SSYR | DSYR | CHER | ZHER (uplo, n, alpha, x, incx, a, lda); CALL SSLR1 | DSLR1 (n, alpha, x, incx, ap); |
If uplo = 'U', A is stored in upper-packed or upper storage mode.
If uplo = 'L', A is stored in lower-packed or lower storage mode.
Specified as: a single character. It must be 'U' or 'L'.
For SSPR, DSPR, CHPR, ZHPR, SSYR, DSYR, CHER, and ZHER, incx < 0 or incx > 0.
For SSLR1 and DSLR1, incx can have any value.
For SSPR and DSPR, ap is the real symmetric matrix A of order n, stored in upper- or lower-packed storage mode.
For CHPR and ZHPR, ap is the complex Hermitian matrix A of order n, stored in upper- or lower-packed storage mode.
For SSLR1 and DSLR1, ap is the real symmetric matrix A of order n, stored in lower-packed storage mode.
Specified as: a one-dimensional array of (at least) length n(n+1)/2, containing numbers of the data type indicated in Table 65.
For SSYR and DSYR, a is the real symmetric matrix A of order n, stored in upper or lower storage mode.
For CHER and ZHER, a is the complex Hermitian matrix A of order n, stored in upper or lower storage mode.
Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 65.
These subroutines perform the computations described in the two sections below. See references [34], [35], and [79]. If n or alpha is 0, no computation is performed.
For CHPR and CHER, intermediate results are accumulated in long precision. For SSPR, SSYR, and SSLR1, intermediate results are accumulated in long precision on some platforms.
These subroutines compute the rank-one update of a real symmetric matrix:
where:
It is expressed as follows:
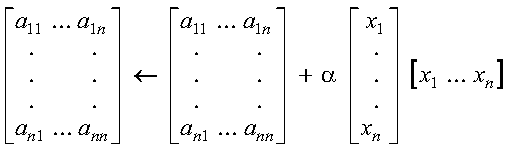
These subroutines compute the rank-one update of a complex Hermitian matrix:
where:
It is expressed as follows:
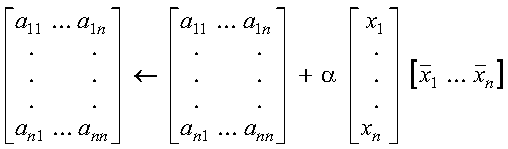
None
This example shows a vector x with a positive stride, and a real symmetric matrix A of order 3, stored in lower-packed storage mode. Matrix A is:
* *
| 8.0 4.0 2.0 |
| 4.0 6.0 7.0 |
| 2.0 7.0 3.0 |
* *
UPLO N ALPHA X INCX AP
| | | | | |
CALL SSPR( 'L' , 3 , 1.0 , X , 1 , AP )
X = (3.0, 2.0, 1.0)
AP = (8.0, 4.0, 2.0, 6.0, 7.0, 3.0)
AP = (17.0, 10.0, 5.0, 10.0, 9.0, 4.0)
This example shows a vector x with a negative stride, and a real symmetric matrix A of order 3, stored in upper-packed storage mode. It uses the same input matrix A as in Example 1.
UPLO N ALPHA X INCX AP
| | | | | |
CALL SSPR( 'U' , 3 , 1.0 , X , -2 , AP )
X = (1.0, . , 2.0, . , 3.0)
AP = (8.0, 4.0, 6.0, 2.0, 7.0, 3.0)
AP = (17.0, 10.0, 10.0, 5.0, 9.0, 4.0)
This example shows a vector x with a positive stride, and a complex Hermitian matrix A of order 3, stored in lower-packed storage mode. Matrix A is:
* *
| (1.0, 0.0) (3.0, 5.0) (2.0, -3.0) |
| (3.0, -5.0) (7.0, 0.0) (4.0, -8.0) |
| (2.0, 3.0) (4.0, 8.0) (6.0, 0.0) |
* *
UPLO N ALPHA X INCX AP
| | | | | |
CALL CHPR( 'L' , 3 , 1.0 , X , 1 , AP )
X = ((1.0, 2.0), (4.0, 0.0), (3.0, 4.0))
AP = ((1.0, . ), (3.0, -5.0), (2.0, 3.0), (7.0, . ),
(4.0, 8.0), (6.0, . ))
AP = ((6.0, 0.0), (7.0, -13.0), (13.0, 1.0), (23.0, 0.0),
(16.0, 24.0), (31.0, 0.0))
This example shows a vector x with a negative stride, and a complex Hermitian matrix A of order 3, stored in upper-packed storage mode. It uses the same input matrix A as in Example 3.
UPLO N ALPHA X INCX AP
| | | | | |
CALL CHPR( 'U' , 3 , 1.0 , X , -2 , AP )
X = ((3.0, 4.0), . , (4.0, 0.0), . , (1.0, 2.0))
AP = ((1.0, . ), (3.0, 5.0), (7.0, . ), (2.0, -3.0),
(4.0, -8.0), (6.0, . ))
AP = ((6.0, 0.0), (7.0, 13.0), (23.0, 0.0), (13.0, -1.0),
(16.0, -24.0), (31.0, 0.0))
This example shows a vector x with a positive stride, and a real symmetric matrix A of order 3, stored in lower storage mode. It uses the same input matrix A as in Example 1.
UPLO N ALPHA X INCX A LDA
| | | | | | |
CALL SSYR( 'L' , 3 , 1.0 , X , 1 , A , 3 )
X = (3.0, 2.0, 1.0)
* *
| 8.0 . . |
A = | 4.0 6.0 . |
| 2.0 7.0 3.0 |
* *
* *
| 17.0 . . |
A = | 10.0 10.0 . |
| 5.0 9.0 4.0 |
* *
This example shows a vector x with a negative stride, and a real symmetric matrix A of order 3, stored in upper storage mode. It uses the same input matrix A as in Example 1.
UPLO N ALPHA X INCX A LDA
| | | | | | |
CALL SSYR( 'U' , 3 , 1.0 , X , -2 , A , 4 )
X = (1.0, . , 2.0, . , 3.0)
* *
| 8.0 4.0 2.0 |
A = | . 6.0 7.0 |
| . . 3.0 |
| . . . |
* *
* *
| 17.0 10.0 5.0 |
A = | . 10.0 9.0 |
| . . 4.0 |
| . . . |
* *
This example shows a vector x with a positive stride, and a complex Hermitian matrix A of order 3, stored in lower storage mode. It uses the same input matrix A as in Example 3.
UPLO N ALPHA X INCX A LDA
| | | | | | |
CALL CHER( 'L' , 3 , 1.0 , X , 1 , A , 3 )
X = ((1.0, 2.0), (4.0, 0.0), (3.0, 4.0))
* *
| (1.0, . ) . . |
A = | (3.0, -5.0) (7.0, . ) . |
| (2.0, 3.0) (4.0, 8.0) (6.0, . ) |
* *
* *
| (6.0, 0.0) . . |
A = | (7.0, -13.0) (23.0, 0.0) . |
| (13.0, 1.0) (16.0, 24.0) (31.0, 0.0) |
* *
This example shows a vector x with a negative stride, and a complex Hermitian matrix A of order 3, stored in upper storage mode. It uses the same input matrix A as in Example 3.
UPLO N ALPHA X INCX A LDA
| | | | | | |
CALL CHER( 'U' , 3 , 1.0 , X , -2 , A , 3 )
X = ((3.0, 4.0), . , (4.0, 0.0), . , (1.0, 2.0))
* *
| (1.0, . ) (3.0, 5.0) (2.0, -3.0) |
A = | . (7.0, . ) (4.0, -8.0) |
| . . (6.0, . ) |
* *
* *
| (6.0, 0.0) (7.0, 13.0) (13.0, -1.0) |
A = | . (23.0, 0.0) (16.0, -24.0) |
| . . (31.0, 0.0) |
* *
This example shows a vector x with a positive stride, and a real symmetric matrix A of order 3, stored in lower-packed storage mode. It uses the same input matrix A as in Example 1.
N ALPHA X INCX AP
| | | | |
CALL SSLR1( 3 , 1.0 , X , 1 , AP )
X = (3.0, 2.0, 1.0)
AP = (8.0, 4.0, 2.0, 6.0, 7.0, 3.0)
AP = (17.0, 10.0, 5.0, 10.0, 9.0, 4.0)