Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SSPR, DSPR, CHPR, ZHPR, SSYR, DSYR, CHER, ZHER, SSLR1, and DSLR1 --Rank-One Update of a Real Symmetric or Complex Hermitian Matrix

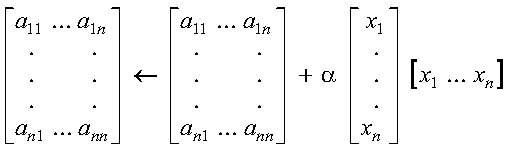
SSPR, DSPR, SSYR, DSYR, SSLR1, and DSLR1 compute the rank-one update of a real symmetric matrix, using the scalar alpha, matrix A, vector x, and its transpose x^T:

A<--A+alphaxx^T

CHPR, ZHPR, CHER, and ZHER compute the rank-one update of a complex Hermitian matrix, using the scalar alpha, matrix A, vector x, and its conjugate transpose x^H:

A<--A+alphaxx^H

The following storage modes are used:

• For SSPR, DSPR, CHPR, and ZHPR, matrix A is stored in upper- or lower-packed storage mode.
• For SSYR, DSYR, CHER, and ZHER, matrix A is stored in upper or lower storage mode.
• For SSLR1 and DSLR1, matrix A is stored in lower-packed storage mode.

Table 65. Data Types

Note:

SSPR and DSPR are Level 2 BLAS subroutines. You should use these subroutines instead of SSLR1 and DSLR1, which are only provided for compatibility with earlier releases of ESSL.

Syntax

On Entry

uplo

indicates the storage mode used for matrix A, where:

If uplo = 'U', A is stored in upper-packed or upper storage mode.

If uplo = 'L', A is stored in lower-packed or lower storage mode.

Specified as: a single character. It must be 'U' or 'L'.

n

is the number of elements in vector x and the order of matrix A. Specified as: a fullword integer; n >= 0.

alpha

is the scaling constant alpha. Specified as: a number of the data type indicated in Table 65.

x

is the vector x of length n. Specified as: a one-dimensional array of (at least) length 1+(n-1)|incx|, containing numbers of the data type indicated in Table 65.

incx

is the stride for vector x. Specified as: a fullword integer, where:

For SSPR, DSPR, CHPR, ZHPR, SSYR, DSYR, CHER, and ZHER, incx < 0 or incx > 0.

For SSLR1 and DSLR1, incx can have any value.

ap

has the following meaning:

For SSPR and DSPR, ap is the real symmetric matrix A of order n, stored in upper- or lower-packed storage mode.

For CHPR and ZHPR, ap is the complex Hermitian matrix A of order n, stored in upper- or lower-packed storage mode.

For SSLR1 and DSLR1, ap is the real symmetric matrix A of order n, stored in lower-packed storage mode.

Specified as: a one-dimensional array of (at least) length n(n+1)/2, containing numbers of the data type indicated in Table 65.

a

has the following meaning:

For SSYR and DSYR, a is the real symmetric matrix A of order n, stored in upper or lower storage mode.

For CHER and ZHER, a is the complex Hermitian matrix A of order n, stored in upper or lower storage mode.

Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 65.

lda

is the leading dimension of the array specified for a. Specified as: a fullword integer; lda > 0 and lda >= n.

On Return

ap

is the matrix A of order n, containing the results of the computation. Returned as: a one-dimensional array, containing numbers of the data type indicated in Table 65.

a

is the matrix A of order n, containing the results of the computation. Returned as: a two-dimensional array, containing numbers of the data type indicated in Table 65.

Notes

1. All subroutines accept lowercase letters for the uplo argument.
2. The vector x must have no common elements with matrix A; otherwise, results are unpredictable. See Concepts.
3. On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <> 0.0, they are set to zero.
4. For a description of how symmetric matrices are stored in upper- or lower-packed storage mode and upper or lower storage mode, see Symmetric Matrix. For a description of how complex Hermitian matrices are stored in upper- or lower-packed storage mode and upper or lower storage mode, see Complex Hermitian Matrix.

Function

These subroutines perform the computations described in the two sections below. See references [34], [35], and [79]. If n or alpha is 0, no computation is performed.

For CHPR and CHER, intermediate results are accumulated in long precision. For SSPR, SSYR, and SSLR1, intermediate results are accumulated in long precision on some platforms.

For SSPR, DSPR, SSYR, DSYR, SSLR1, and DSLR1

These subroutines compute the rank-one update of a real symmetric matrix:

A<--A+alphaxx^T

where:

A is a real symmetric matrix of order n.

alpha is a scalar.

x is a vector of length n.

x^T is the transpose of vector x.

It is expressed as follows:

For CHPR, ZHPR, CHER, and ZHER

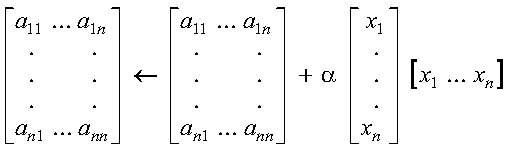
These subroutines compute the rank-one update of a complex Hermitian matrix:

A<--A+alphaxx^H

where:

A is a complex Hermitian matrix of order n.

alpha is a scalar.

x is a vector of length n.

x^H is the conjugate transpose of vector x.

It is expressed as follows:

Error Condition

Computational Errors

None

Input-Argument Errors

1. uplo <>  'L' or 'U'
2. n < 0
3. incx = 0
4. lda <= 0
5. lda < n

Example 1

This example shows a vector x with a positive stride, and a real symmetric matrix A of order 3, stored in lower-packed storage mode. Matrix A is:

                       *               *
                       | 8.0  4.0  2.0 |
                       | 4.0  6.0  7.0 |
                       | 2.0  7.0  3.0 |
                       *               *

Call Statement and Input

          UPLO   N  ALPHA  X  INCX  AP
            |    |    |    |   |    |
CALL SSPR( 'L' , 3 , 1.0 , X , 1  , AP )
 
X        =  (3.0, 2.0, 1.0)
AP       =  (8.0, 4.0, 2.0, 6.0, 7.0, 3.0)

Output

AP       =  (17.0, 10.0, 5.0, 10.0, 9.0, 4.0)

Example 2

This example shows a vector x with a negative stride, and a real symmetric matrix A of order 3, stored in upper-packed storage mode. It uses the same input matrix A as in Example 1.

Call Statement and Input

          UPLO   N  ALPHA  X  INCX  AP
            |    |    |    |    |   |
CALL SSPR( 'U' , 3 , 1.0 , X , -2 , AP )
 
X        =  (1.0, . , 2.0, . , 3.0)
AP       =  (8.0, 4.0, 6.0, 2.0, 7.0, 3.0)

Output

AP       =  (17.0, 10.0, 10.0, 5.0, 9.0, 4.0)

Example 3

This example shows a vector x with a positive stride, and a complex Hermitian matrix A of order 3, stored in lower-packed storage mode. Matrix A is:

              *                                      *
              |  (1.0, 0.0)  (3.0, 5.0)  (2.0, -3.0) |
              | (3.0, -5.0)  (7.0, 0.0)  (4.0, -8.0) |
              |  (2.0, 3.0)  (4.0, 8.0)   (6.0, 0.0) |
              *                                      *

Note:

On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <> 0.0, they are set to zero.

Call Statement and Input

           UPLO  N  ALPHA  X  INCX AP
            |    |    |    |   |   |
CALL CHPR( 'L' , 3 , 1.0 , X , 1 , AP )
 
X        =  ((1.0, 2.0), (4.0, 0.0), (3.0, 4.0))
AP       =  ((1.0, . ), (3.0, -5.0), (2.0, 3.0), (7.0, . ),
             (4.0, 8.0), (6.0, . ))

Output

AP       =  ((6.0, 0.0), (7.0, -13.0), (13.0, 1.0), (23.0, 0.0),
             (16.0, 24.0), (31.0, 0.0))

Example 4

This example shows a vector x with a negative stride, and a complex Hermitian matrix A of order 3, stored in upper-packed storage mode. It uses the same input matrix A as in Example 3.

Note:

On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <> 0.0, they are set to zero.

Call Statement and Input

           UPLO  N  ALPHA  X  INCX  AP
            |    |    |    |    |   |
CALL CHPR( 'U' , 3 , 1.0 , X , -2 , AP )
 
X        =  ((3.0, 4.0), . , (4.0, 0.0), . , (1.0, 2.0))
AP       =  ((1.0, . ), (3.0, 5.0), (7.0, . ), (2.0, -3.0),
             (4.0, -8.0), (6.0, . ))

Output

AP       =  ((6.0, 0.0), (7.0, 13.0), (23.0, 0.0), (13.0, -1.0),
             (16.0, -24.0), (31.0, 0.0))

Example 5

This example shows a vector x with a positive stride, and a real symmetric matrix A of order 3, stored in lower storage mode. It uses the same input matrix A as in Example 1.

Call Statement and Input

           UPLO  N  ALPHA  X  INCX A  LDA
            |    |    |    |   |   |   |
CALL SSYR( 'L' , 3 , 1.0 , X , 1 , A , 3 )
 
X        =  (3.0, 2.0, 1.0)
 
        *               *
        | 8.0   .    .  |
A    =  | 4.0  6.0   .  |
        | 2.0  7.0  3.0 |
        *               *

Output

        *                 *
        | 17.0    .    .  |
A    =  | 10.0  10.0   .  |
        |  5.0   9.0  4.0 |
        *                 *

Example 6

This example shows a vector x with a negative stride, and a real symmetric matrix A of order 3, stored in upper storage mode. It uses the same input matrix A as in Example 1.

Call Statement and Input

           UPLO  N  ALPHA  X  INCX  A  LDA
            |    |    |    |    |   |   |
CALL SSYR( 'U' , 3 , 1.0 , X , -2 , A , 4 )
 
X        =  (1.0, . , 2.0, . , 3.0)
 
        *               *
        | 8.0  4.0  2.0 |
A    =  |  .   6.0  7.0 |
        |  .    .   3.0 |
        |  .    .    .  |
        *               *

Output

        *                 *
        | 17.0  10.0  5.0 |
A    =  |   .   10.0  9.0 |
        |   .     .   4.0 |
        |   .     .    .  |
        *                 *

Example 7

This example shows a vector x with a positive stride, and a complex Hermitian matrix A of order 3, stored in lower storage mode. It uses the same input matrix A as in Example 3.

Note:

On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <> 0.0, they are set to zero.

Call Statement and Input

           UPLO  N  ALPHA  X  INCX A  LDA
            |    |    |    |   |   |   |
CALL CHER( 'L' , 3 , 1.0 , X , 1 , A , 3 )
 
X        =  ((1.0, 2.0), (4.0, 0.0), (3.0, 4.0))
 
        *                                    *
        |   (1.0, . )       .            .   |
A    =  | (3.0, -5.0)   (7.0, . )        .   |
        |  (2.0, 3.0)  (4.0, 8.0)  (6.0, . ) |
        *                                    *

Output

        *                                         *
        |   (6.0, 0.0)        .            .      |
A    =  | (7.0, -13.0)   (23.0, 0.0)       .      |
        |  (13.0, 1.0)  (16.0, 24.0)  (31.0, 0.0) |
        *                                         *

Example 8

This example shows a vector x with a negative stride, and a complex Hermitian matrix A of order 3, stored in upper storage mode. It uses the same input matrix A as in Example 3.

Note:

On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, if alpha <> 0.0, they are set to zero.

Call Statement and Input

           UPLO  N  ALPHA  X  INCX  A  LDA
            |    |    |    |    |   |   |
CALL CHER( 'U' , 3 , 1.0 , X , -2 , A , 3 )
 
X        =  ((3.0, 4.0), . , (4.0, 0.0), . , (1.0, 2.0))
 
        *                                    *
        | (1.0, . )  (3.0, 5.0)  (2.0, -3.0) |
A    =  |     .      (7.0,  . )  (4.0, -8.0) |
        |     .          .         (6.0, . ) |
        *                                    *

Output

        *                                        *
        | (6.0, 0.0)  (7.0, 13.0)   (13.0, -1.0) |
A    =  |     .       (23.0, 0.0)  (16.0, -24.0) |
        |     .            .         (31.0, 0.0) |
        *                                        *

Example 9

This example shows a vector x with a positive stride, and a real symmetric matrix A of order 3, stored in lower-packed storage mode. It uses the same input matrix A as in Example 1.

Call Statement and Input

            N  ALPHA  X  INCX  AP
            |    |    |   |    |
CALL SSLR1( 3 , 1.0 , X , 1  , AP )
 
X        =  (3.0, 2.0, 1.0)
AP       =  (8.0, 4.0, 2.0, 6.0, 7.0, 3.0)

Output

AP       =  (17.0, 10.0, 5.0, 10.0, 9.0, 4.0)