Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference
DBSTRF factors a real symmetric indefinite matrix A. The
matrix A, stored in upper- or lower-packed storage mode, is
factored using the Bunch-Kaufman diagonal pivoting method, where A
is expressed as:
- A = UDUT or
- A = LDLT
where:
- U is a product of permutation and unit upper triangular
matrices.
- L is a product of permutation and unit lower triangular
matrices.
- D is a symmetric block diagonal matrix, consisting of
1 × 1 and 2 × 2 diagonal blocks.
To solve a system of equations with one or more right-hand sides, follow
the call to this subroutine with one or more calls to DBSTRS.
Table 98. Data Types
| A
| ipvt
| Subroutine
|
| Long-precision real
| Integer
| DBSTRF
|
- Note:
- The output from DBSTRF should be used only as input to DBSTRS, for performing
a solve.
| Fortran
| CALL DBSTRF (uplo, n, ap, ipvt,
nsinfo)
|
| C and C++
| dbstrf (uplo, n, ap, ipvt,
nsinfo);
|
| PL/I
| CALL DBSTRF (uplo, n, ap, ipvt,
nsinfo);
|
- uplo
- indicates whether matrix A is stored in upper- or lower-packed
storage mode, where:
If uplo = 'U', A is stored in
upper-packed storage mode.
If uplo = 'L', A is stored in
lower-packed storage mode.
Specified as: a single character. It must be 'U' or
'L'.
- n
- is the order n of matrix A.
Specified as: a fullword integer;
n >= 0.
- ap
- is array, referred to as AP, in which matrix A, to
be factored, is stored in upper- or lower-packed storage mode.
Specified as: a one-dimensional array of length nsinfo,
containing numbers of the data type indicated in Table 98. See Notes.
- ipvt
- See On Return.
- nsinfo
- is the number of elements in array, AP.
If n <= nco,
nsinfo = n(n + 1) / 2
Where:
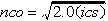
- ics is the size in doublewords of the data cache. The data
cache size can be obtained by utilizing the following C language code
fragment:
#include <sys/systemcfg.h>
int ics;
.
.
.
ics=_system_configuration.dcache_size/8;
Otherwise, to determine a sufficient amount of storage, use the following
processor-independent formula:
- n0 = 100
- ns = (n + n0) (n + n0
+ 1) / 2 + n(n0)
- For uplo = 'L',
- nsinfo >= ns
- For uplo = 'U',
- n1 = (n + 1) / 2
- nt = n((n + 1) / 2)
- nt1 = n1(n1 + 1)
- ns1 = nt + nt1
- nsinfo >= max(ns, ns1)
To determine the minimal amount of storage see Notes.
Specified as: a fullword integer;
nsinfo > 0.
- ap
- is the transformed matrix A of order n, containing the
results of the factorization.
If nsinfo >= 0 and n > nco,
additional information that can be used to obtain a minimum nsinfo is
stored in AP(1). See Notes and Function.
Returned as: a one-dimensional array, containing numbers of the data
type indicated in Table 98.
- ipvt
- is an integer vector of length n, containing the pivot
information necessary to construct the factored form of A.
Returned as: a one-dimensional array of (at least) length n,
containing numbers of the data type indicated in Table 98.
- nsinfo
- indicates the result of the computation.
- If nsinfo = 0, the factorization completed
successfully.
- If nsinfo > 0, factorization was unsuccessful and
nsinfo is set toi where dii
is exactly zero.
- If nsinfo < 0, factorization did not take place and
the array AP remains unchanged. |nsinfo| is the
minimal storage required for factorization to take place. Error message
2200 is issued and execution terminates, unless you have used ERRSET to make
error code 2200 recoverable. See What Can You Do about ESSL Input-Argument Errors?.
Specified as: a fullword integer.
- This subroutine accepts lowercase letters for the uplo
argument.
- In your C program, argument nsinfo must be passed by
reference.
- In the input array specified for ap, the first
n(n+1)/2 elements are matrix elements. The additional
locations, required in the array, are used for working storage.
- The array specified for ap should not be altered between calls to
the factorization and solve subroutines; otherwise, unpredictable results
may occur.
- On return, if nsinfo >= 0 and
n > nco, ap contains additional
information in AP(1) that can be used to obtain the minimal
required nsinfo. This information can be accessed using the
following code fragment:
REAL*8 AP(NSINFO)
INTEGER API(2)
EQUIVALENCE(API, AP)
.
.
.
NSINFOMIN = API(2)
- For a description of how a symmetric matrix is stored in upper- or
lower-packed storage mode in an array, see Symmetric Matrix.
A real symmetric indefinite matrix A, stored in upper- or
lower-packed storage mode, is factored using the Bunch-Kaufman diagonal
pivoting method, where A is expressed as:
- A = UDUT or
- A = LDLT
where:
- U is a product of permutation and unit upper triangular
matrices.
- L is a product of permutation and unit lower triangular
matrices.
- D is a symmetric block diagonal matrix, consisting of
1 × 1 and 2 × 2 diagonal blocks.
If n is 0, no computation is performed and the subroutine returns
after doing some parameter checking.
See references [8] and [65].
None.
Matrix A is singular.
- The factorization completed but the block diagonal matrix D is
exactly singular. nsinfo is set to i, where
dii is exactly zero. This diagonal
element is identified in the computational error message.
- The computational error message may occur multiple times with processing
continuing after each error, because the default for the number of allowable
errors for error code 2147 is set to be unlimited in the ESSL error option
table. For details, see What Can You Do about ESSL Computational Errors?.
- uplo <> 'U' or 'L'
- n < 0
- nsinfo < (minimum value).
- For the minimum value, see the nsinfo argument
description.
- Return code 1 is returned if error 2200 is recoverable.
This example shows a factorization of a symmetric indefinite matrix
A of order 8, stored in lower-packed storage mode, where on input
matrix A is:
* *
| 3.0 5.0 -2.0 2.0 3.0 -5.0 -2.0 -3.0 |
| 5.0 3.0 2.0 -2.0 5.0 -3.0 2.0 -5.0 |
| -2.0 2.0 0.0 0.0 -2.0 2.0 0.0 6.0 |
| 2.0 -2.0 0.0 8.0 -6.0 -10.0 -8.0 -14.0 |
| 3.0 5.0 -2.0 -6.0 12.0 6.0 8.0 6.0 |
| -5.0 -3.0 2.0 -10.0 6.0 16.0 8.0 20.0 |
| -2.0 2.0 0.0 -8.0 8.0 8.0 6.0 18.0 |
| -3.0 -5.0 6.0 -14.0 6.0 20.0 18.0 34.0 |
* *
- Note:
- The AP array is formatted in a triangular arrangement for
readability; however, it is stored in lower-packed storage mode.
UPLO N AP IPVT NSINFO
| | | | |
CALL DBSTRF ( 'L', 8, AP, IPVT, 36 )
AP = ( 3.0, 5.0, -2.0, 2.0, 3.0, -5.0, -2.0, -3.0,
3.0, 2.0, -2.0, 5.0, -3.0, 2.0, -5.0,
0.0, 0.0, -2.0, 2.0, 0.0, 6.0,
8.0, -6.0,-10.0, -8.0,-14.0,
12.0, 6.0, 8.0, 6.0,
16.0, 8.0, 20.0,
6.0, 18.0,
34.0 )
NSINFO = 0
- Note:
- AP and IPVT are stored in an internal format
and must be passed unchanged to the solve subroutine.
This example shows a factorization of a symmetric indefinite matrix
A of order 8, stored in upper-packed storage mode, where on input
matrix A is:
* *
| 34.0 18.0 17.0 6.0 -14.0 6.0 -5.0 -3.0 |
| 18.0 6.0 6.0 8.0 -8.0 0.0 2.0 -2.0 |
| 17.0 6.0 9.0 9.0 -8.0 0.0 2.0 -2.0 |
| 6.0 8.0 9.0 12.0 -6.0 -2.0 5.0 3.0 |
|-14.0 -8.0 -8.0 -6.0 8.0 0.0 -2.0 2.0 |
| 6.0 0.0 0.0 -2.0 0.0 0.0 2.0 -2.0 |
| -5.0 2.0 2.0 5.0 -2.0 2.0 3.0 5.0 |
| -3.0 -2.0 -2.0 3.0 2.0 -2.0 5.0 3.0 |
* *
- Note:
- The AP array is formatted in a triangular arrangement for
readability; however, it is stored in upper-packed storage mode.
UPLO N AP IPVT NSINFO
| | | | |
CALL DBSTRF ( 'U', 8, AP, IPVT, 36 )
AP = ( 34.0,
18.0, 6.0,
17.0, 6.0, 9.0,
6.0, 8.0, 9.0, 12.0,
-14.0, -8.0, -8.0, -6.0, 8.0,
6.0, 0.0, 0.0, -2.0, 0.0, 0.0,
-5.0, 2.0, 2.0, 5.0, -2.0, 2.0, 3.0,
-3.0, -2.0, -2.0, 3.0, 2.0, -2.0, 5.0, 3.0 )
NSINFO = 0
- Note:
- AP and IPVT are stored in an internal format and must
be passed unchanged to the solve subroutine.
[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]