Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

DBSSV--Symmetric Indefinite Matrix Factorization and Multiple Right-Hand Side Solve

The DBSSV subroutine solves a system of linear equations AX = B for X, where A is a real symmetric indefinite matrix, and X and B are real general matrices.

The matrix A, stored in upper- or lower-packed storage mode, is factored using the Bunch-Kaufman diagonal pivoting method, where A is expressed as:

A = UDU^T or

A = LDL^T

where:

U is a product of permutation and unit upper triangular matrices.

L is a product of permutation and unit lower triangular matrices.

D is a symmetric block diagonal matrix, consisting of 1 × 1 and 2 × 2 diagonal blocks.

Table 97. Data Types

A, B	*ipvt*	Subroutine
Long-precision real	Integer	DBSSV

Syntax

Fortran	CALL DBSSV (`uplo`, `n`, `nrhs`, `ap`, `ipvt`, `b`, `ldb`, `nsinfo`)
C and C++	dbssv (`uplo`, `n`, `nrhs`, `ap`, `ipvt`, `b`, `ldb`, `nsinfo`);
PL/I	CALL DBSSV (`uplo`, `n`, `nrhs`, `ap`, `ipvt`, `b`, `ldb`, `nsinfo`);

On Entry

uplo

indicates whether matrix A is stored in upper- or lower-packed storage mode, where:

If uplo = 'U', A is stored in upper-packed storage mode.

If uplo = 'L', A is stored in lower-packed storage mode.

Specified as: a single character. It must be 'U' or 'L'.

n

is the order n of matrix A and the number of rows of matrix B.

Specified as: a fullword integer; n >= 0.

nrhs

is the number of right-hand sides; i.e., the number of columns of matrix B.

Specified as: a fullword integer; nrhs >= 0.

ap

is array, referred to as AP, in which matrix A, to be factored, is stored in upper- or lower-packed storage mode.

Specified as: a one-dimensional array of length nsinfo, containing numbers of the data type indicated in Table 97. See Notes.

ipvt

See On Return.

b

is the matrix B, containing the nrhs right-hand sides of the system. The right-hand sides, each of length n, reside in the columns of matrix B.

Specified as: an ldb by (at least) nrhs array, containing numbers of the data type indicated in Table 97.

ldb

is the leading dimension of the array specified for B.

Specified as: a fullword integer; ldb > 0 and ldb >= n.

nsinfo

is the number of elements in array, AP.

If n <= nco, nsinfo = n(n + 1) / 2

Where:

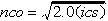
Math Graphic

ics is the size in doublewords of the data cache. The data cache size can be obtained by utilizing the following C language code fragment:

#include <sys/systemcfg.h>
int ics;
     .
     .
     .
ics=_system_configuration.dcache_size/8;

Otherwise, to determine a sufficient amount of storage, use the following processor-independent formula:

n0 = 100

ns = (n + n0) (n + n0 + 1) / 2 + n(n0)

For uplo = 'L',

nsinfo >= ns

For uplo = 'U',

n1 = (n + 1) / 2

nt = n((n + 1) / 2)

nt1 = n1(n1 + 1)

ns1 = nt + nt1

nsinfo >= max(ns, ns1)

To determine the minimal amount of storage see Notes.

Specified as: a fullword integer; nsinfo > 0.

On Return

ap

is the transformed matrix A of order n, containing the results of the factorization.

If nsinfo >= 0 and n > nco, additional information that can be used to obtain a minimum nsinfo is stored in AP(1). See Notes and Function.

Returned as: a one-dimensional array, containing numbers of the data type indicated in Table 97.

ipvt

is an integer vector of length n, containing the pivot information necessary to construct the factored form of A.

Returned as: a one-dimensional array of (at least) length n, containing numbers of the data type indicated in Table 97.

b

is the matrix B, containing the nrhs solutions to the system in the columns of B.

Returned as: an ldb by (at least) nrhs array, containing numbers of the data type indicated in Table 97.

nsinfo

indicates the result of the computation.

If nsinfo = 0, the subroutine completed successfully.
If nsinfo > 0, factorization was unsuccessful and array B was not updated. nsinfo is set to i where d_ii is exactly zero.
If nsinfo < 0, factorization did not take place and the arrays, AP and B, remain unchanged. |nsinfo| is the minimal storage required for factorization to take place. Error message 2200 is issued and execution terminates, unless you have used ERRSET to make error code 2200 recoverable. See What Can You Do about ESSL Input-Argument Errors?.

Specified as: a fullword integer.

Notes

This subroutine accepts lowercase letters for the uplo argument.
In your C program, argument nsinfo must be passed by reference.
In the input array specified for ap, the first n(n+1)/2 elements are matrix elements. The additional locations, required in the array, are used for working storage.
The vectors and matrices used in this computation must have no common elements; otherwise, results are unpredictable. See Concepts.
On return, if nsinfo >= 0 and n > nco, ap contains additional information in AP(1) that can be used to obtain the minimal required nsinfo. This information can be accessed using the following code fragment:
```
REAL*8	AP(NSINFO)
INTEGER	API(2)
EQUIVALENCE(API, AP)
          .
          .
          .
NSINFOMIN = API(2)
```
For a description of how a symmetric matrix is stored in upper- or lower-packed storage mode in an array, see Symmetric Matrix.

Function

The system AX = B is solved for X, where A is a real symmetric indefinite matrix, and X and B are real general matrices.

The matrix A, stored in upper- or lower-packed storage mode, is factored using the Bunch-Kaufman diagonal pivoting method, where A is expressed as:

A = UDU^T or

A = LDL^T

where:

U is a product of permutation and unit upper triangular matrices.

L is a product of permutation and unit lower triangular matrices.

D is a symmetric block diagonal matrix, consisting of 1 × 1 and 2 × 2 diagonal blocks.

If n or nrhs is 0, no computation is performed and the subroutine returns after doing some parameter checking.

See references [8] and [65].

Error Conditions

Computational Errors

Matrix A is singular.

The factorization completed but the block diagonal matrix D is exactly singular. nsinfo is set to i, where d_ii is exactly zero. This diagonal element is identified in the computational error message.
The computational error message may occur multiple times with processing continuing after each error, because the default for the number of allowable errors for error code 2147 is set to be unlimited in the ESSL error option table. For details, see What Can You Do about ESSL Computational Errors?.

Input-Argument Errors

uplo <> 'U' or 'L'
n < 0
n > ldb
ldb <= 0
nrhs < 0
nsinfo < (minimum value).
- For the minimum value, see the nsinfo argument description.
- Return code 1 is returned if error 2200 is recoverable.

This example shows how to solve the system AX = B, for three right-hand sides, where matrix A is a real symmetric indefinite matrix of order 8, stored in lower-packed storage mode, and X and B are real general matrices.

On input, matrix A is:

             *                                                *
             |  3.0   5.0  -2.0   2.0   3.0  -5.0  -2.0  -3.0 |
             |  5.0   3.0   2.0  -2.0   5.0  -3.0   2.0  -5.0 |
             | -2.0   2.0   0.0   0.0  -2.0   2.0   0.0   6.0 |
A =          |  2.0  -2.0   0.0   8.0  -6.0 -10.0  -8.0 -14.0 |
             |  3.0   5.0  -2.0  -6.0  12.0   6.0   8.0   6.0 |
             | -5.0  -3.0   2.0 -10.0   6.0  16.0   8.0  20.0 |
             | -2.0   2.0   0.0  -8.0   8.0   8.0   6.0  18.0 |
             | -3.0  -5.0   6.0 -14.0   6.0  20.0  18.0  34.0 |
             *                                                *

Note:: The AP array is formatted in a triangular arrangement for readability; however, it is stored in lower-packed storage mode.

Call Statement and Input

             UPLO  N   NRHS  AP  IPVT  B  LDB  NSINFO
              |    |    |     |   |    |   |     |
CALL DBSSV ( 'L',  8,   3,   AP, IPVT, B,  8,   36  )

AP = ( 3.0,  5.0, -2.0,  2.0,  3.0, -5.0, -2.0, -3.0,
       3.0,  2.0, -2.0,  5.0, -3.0,  2.0, -5.0,
       0.0,  0.0, -2.0,  2.0,  0.0,  6.0,
       8.0, -6.0,-10.0, -8.0,-14.0,
      12.0,  6.0,  8.0,  6.0,
      16.0,  8.0, 20.0,
       6.0, 18.0,
      34.0 )

        *                     *
        |   1.0  -38.0   47.0 |
        |   7.0  -10.0   73.0 |
        |   6.0   52.0    2.0 |
B    =  | -30.0 -228.0  -42.0 |
        |  32.0  183.0  105.0 |
        |  34.0  297.0    9.0 |
        |  32.0  244.0   44.0 |
        |  62.0  497.0   61.0 |
        *                     *

Output

        *                     *
        |   1.0    1.0    8.0 |
        |   1.0    2.0    7.0 |
        |   1.0    3.0    6.0 |
B    =  |   1.0    4.0    5.0 |
        |   1.0    5.0    4.0 |
        |   1.0    6.0    3.0 |
        |   1.0    7.0    2.0 |
        |   1.0    8.0    1.0 |
        *                     *

NSINFO = 0

Note:: AP and IPVT are stored in an internal format.

Example 2

This example shows how to solve the system AX = B, for three right-hand sides, where matrix A is a real symmetric indefinite matrix of order 8, stored in upper-packed storage mode, and X and B are real general matrices.

On input, matrix A is:

             *                                                *
             | 34.0  18.0  17.0   6.0 -14.0   6.0  -5.0  -3.0 |
             | 18.0   6.0   6.0   8.0  -8.0   0.0   2.0  -2.0 |
             | 17.0   6.0   9.0   9.0  -8.0   0.0   2.0  -2.0 |
             |  6.0   8.0   9.0  12.0  -6.0  -2.0   5.0   3.0 |
             |-14.0  -8.0  -8.0  -6.0   8.0   0.0  -2.0   2.0 |
             |  6.0   0.0   0.0  -2.0   0.0   0.0   2.0  -2.0 |
             | -5.0   2.0   2.0   5.0  -2.0   2.0   3.0   5.0 |
             | -3.0  -2.0  -2.0   3.0   2.0  -2.0   5.0   3.0 |
             *                                                *

Note:: The AP array is formatted in a triangular arrangement for readability; however, it is stored in upper-packed storage mode.

Call Statement and Input

             UPLO  N   NRHS  AP  IPVT  B  LDB  NSINFO
              |    |    |     |   |    |   |     |
CALL DBSSV ( 'U',  8,   3,   AP, IPVT, B,  8,   36  )

AP = ( 34.0,
       18.0,  6.0,
       17.0,  6.0,  9.0,
        6.0,  8.0,  9.0, 12.0,
      -14.0, -8.0, -8.0, -6.0,  8.0,
        6.0,  0.0,  0.0, -2.0,  0.0,  0.0,
       -5.0,  2.0,  2.0,  5.0, -2.0,  2.0,  3.0,
       -3.0, -2.0, -2.0,  3.0,  2.0, -2.0,  5.0,  3.0 )

        *                     *
        |  59.0   52.0  479.0 |
        |  30.0   38.0  232.0 |
        |  33.0   50.0  247.0 |
B    =  |  35.0  114.0  201.0 |
        | -28.0  -36.0 -216.0 |
        |   4.0   -4.0   40.0 |
        |  12.0   88.0   20.0 |
        |   4.0   56.0  -20.0 |
        *                     *

Output

        *                     *
        |   1.0    1.0    8.0 |
        |   1.0    2.0    7.0 |
        |   1.0    3.0    6.0 |
B    =  |   1.0    4.0    5.0 |
        |   1.0    5.0    4.0 |
        |   1.0    6.0    3.0 |
        |   1.0    7.0    2.0 |
        |   1.0    8.0    1.0 |
        *                     *

NSINFO = 0

Note:: AP and IPVT are stored in an internal format.

[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]

Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

DBSSV--Symmetric Indefinite Matrix Factorization and Multiple Right-Hand Side Solve

Syntax

On Entry

On Return

Notes

Function

Error Conditions

Resource Errors

Computational Errors

Input-Argument Errors

Example 1

Call Statement and Input

Output

Example 2

Call Statement and Input

Output