Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SCONF and SCORF--Convolution or Correlation of One Sequence with One or More Sequences Using the Mixed-Radix Fourier Method

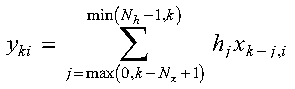
These subroutines compute the convolutions and correlations, respectively, of a sequence with one or more sequences using the mixed-radix Fourier method. The input and output sequences contain short-precision real numbers.

Note:

Two invocations of these subroutines are necessary: one to prepare the working storage for the subroutine, and the other to perform the computations.

Syntax

On Entry

init

is a flag, where:

If init <> 0, trigonometric functions, the transform of the sequence in h, and other parameters, depending on arguments other than x, are computed and saved in aux1. The contents of x and y are not used or changed.

If init = 0, the convolutions or correlations of the sequence that was in h at initialization with the sequences in x are computed. h is not used or changed. The only arguments that may change after initialization are x, y, and aux2. All scalar arguments must be the same as when the subroutine was called for initialization with init <> 0.

Specified as: a fullword integer. It can have any value.

h

is the array H, consisting of the sequence of length N_h to be convolved or correlated with the sequences in array X. Specified as: an array of (at least) length 1+(N_h-1)|inc1h|, containing short-precision real numbers.

inc1h

is the stride between the elements within the sequence in array H. Specified as: a fullword integer; inc1h > 0.

x

is the array X, consisting of m input sequences of length N_x, each to be convolved or correlated with the sequence in array H. Specified as: an array of (at least) length 1+(N_x-1)inc1x+(m-1)inc2x, containing short-precision real numbers.

inc1x

is the stride between the elements within each sequence in array X. Specified as: a fullword integer; inc1x > 0.

inc2x

is the stride between the first elements of the sequences in array X. Specified as: a fullword integer; inc2x > 0.

y

See On Return.

inc1y

is the stride between the elements within each sequence in output array Y. Specified as: a fullword integer; inc1y > 0.

inc2y

is the stride between the first elements of each sequence in output array Y. Specified as: a fullword integer; inc2y > 0.

nh

is the number of elements, N_h, in the sequence in array H. Specified as: a fullword integer; N_h > 0.

nx

is the number of elements, N_x, in each sequence in array X. Specified as: a fullword integer; N_x > 0.

m

is the number of sequences in array X to be convolved or correlated. Specified as: a fullword integer; m > 0.

iy0

is the convolution or correlation index of the element to be stored in the first position of each sequence in array Y. Specified as: a fullword integer. It can have any value.

ny

is the number of elements, N_y, in each sequence in array Y. Specified as: a fullword integer; N_y > 0.

aux1

is the working storage for this subroutine, where:

If init <> 0, the working storage is computed.

If init = 0, the working storage is used in the computation of the convolutions.

Specified as: an area of storage, containing naux1 long-precision real numbers.

naux1

is the number of doublewords in the working storage specified in aux1. Specified as: a fullword integer; naux1 > 23 and naux1 >= (minimum value required for successful processing). To determine a sufficient value, use the processor-independent formulas. For values between 23 and the minimum value, you have the option of having the minimum value returned in this argument. For details, see Using Auxiliary Storage in ESSL.

aux2

has the following meaning:

If naux2 = 0 and error 2015 is unrecoverable, aux2 is ignored.

Otherwise, it is the working storage used by this subroutine, which is available for use by the calling program between calls to this subroutine.

Specified as: an area of storage, containing naux2 long-precision real numbers. On output, the contents are overwritten.

naux2

is the number of doublewords in the working storage specified in aux2. Specified as: a fullword integer, where:

If naux2 = 0 and error 2015 is unrecoverable, SCONF and SCORF dynamically allocate the work area used by the subroutine. The work area is deallocated before control is returned to the calling program.

Otherwise, naux2 >= (minimum value required for successful processing). To determine a sufficient value, use the processor-independent formulas. For all other values specified less than the minimum value, you have the option of having the minimum value returned in this argument. For details, see Using Auxiliary Storage in ESSL.

On Return

y

has the following meaning, where:

If init <> 0, this argument is not used, and its contents remain unchanged.

If init = 0, this is array Y, consisting of m output sequences of length N_y that are the result of the convolutions or correlations of the sequence in array H with the sequences in array X.

Returned as: an array of (at least) length 1+(N_y-1)inc1y+(m-1)inc2y, containing short-precision real numbers.

aux1

is the working storage for this subroutine, where:

If init <> 0, it contains information ready to be passed in a subsequent invocation of this subroutine.

If init = 0, its contents are unchanged.

Returned as: the contents are not relevant.

Notes

1. aux1 should not be used by the calling program between calls to this subroutine with init <> 0 and init = 0. However, it can be reused after intervening calls to this subroutine with different arguments.
2. When using the ESSL SMP library, for optimal performance, the number of threads specified should be the same for init <> 0 and init = 0.
3. If you specify the same array for X and Y, then inc1x and inc1y must be equal, and inc2x and inc2y must be equal. In this case, output overwrites input.
4. If you specify different arrays for X and Y, they must have no common elements; otherwise, results are unpredictable. See Concepts.
5. If iy0 and ny are such that output outside the basic range is needed, the subroutine stores zeros. These ranges are: 0 <= k <= N_x+N_h-2 for SCONF and 1-N_h <= k <= N_x-1 for SCORF.

Formulas for the Length of the Fourier Transform

Before calculating the necessary sizes of naux1 and naux2, you must determine the length n of the Fourier transform. The value of n is based on nf. You can use one of two techniques to determine nf:

• Use the simple overestimate of nf = nx+nh-1. (If iy0 = 0 and ny > nh+nx, this is the actual value, not an overestimate.)
• Use the values of the arguments iy0, nh, nx, and ny inserted into the following formulas to get a value for the variable nf:

  iy0p = max(iy0, 0)

  ix0 = max((iy0p+1)-nh, 0)

  ih0 = max((iy0p+1)-nx, 0)

  nd = ix0+ih0

  n1 = iy0+ny

  nxx = min(n1, nx)-ix0

  nhh = min(n1, nh)-ih0

  ntt = nxx+nhh-1

  nn1 = n1-nd

  iyy0 = iy0p-nd

  nzleft = max(0, nhh-iyy0-1)

  nzrt = min(nn1, ntt)-nxx

  nf = max(12, nxx+max(nzleft, nzrt))

After calculating the value for nf, using one of these two techniques, refer to the formula or table of allowable values of n in Acceptable Lengths for the Transforms, selecting the value equal to or greater than nf.

Processor-Independent Formulas for NAUX1 and NAUX2

The required values of naux1 and naux2 depend on the value determined for n in Formulas for the Length of the Fourier Transform.

NAUX1 Formulas

If n <= 16384, use naux1 = 58000.

If n > 16384, use naux1 = 40000+2.14n.

NAUX2 Formulas

If n <= 16384, use naux2 = 30000.

If n > 16384, use naux2 = 20000+1.07n.

Function

The convolutions and correlations of a sequence in array H with one or more sequences in array X are expressed as follows.

Convolutions for SCONF:

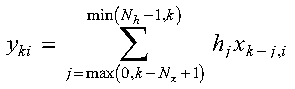
Correlations for SCORF:

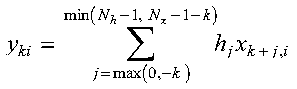
for:

k = iy0, iy0+1, ..., iy0+N_y-1

i = 1, 2, ..., m

where:

y_ki are elements of the m sequences of length N_y in array Y.

x_ki are elements of the m sequences of length N_x in array X.

h_j are elements of the sequence of length N_h in array H.

iy0 is the convolution or correlation index of the element to be stored in the first position of each sequence in array Y.

min and max select the minimum and maximum values, respectively.

These subroutines use a Fourier transform method with a mixed-radix capability. This provides maximum performance for your application. The length of the transform, n, that you must calculate to determine the correct sizes for naux1 and naux2 is the same length used by the Fourier transform subroutines called by this subroutine. It is assumed that elements outside the range of definition are zero. See references [17] and [84].

Two invocations of this subroutine are necessary:

1. With init <> 0, the subroutine tests and initializes arguments of the program, setting up the aux1 working storage.
2. With init = 0, the subroutine checks that the initialization arguments in the aux1 working storage correspond to the present arguments, and if so, performs the calculation of the convolutions.

Error Conditions

Resource Errors

Error 2015 is unrecoverable, naux2 = 0, and unable to allocate work area.

Computational Errors

None

Input-Argument Errors

1. nh, nx, ny, or m <= 0
2. inc1h, inc1x, inc2x, inc1y, or inc2y <= 0
3. The resulting internal Fourier transform length n, is too large. See Convolutions and Correlations by Fourier Methods.
4. The subroutine has not been initialized with the present arguments.
5. naux1 <= 23
6. naux1 is too small--that is, less than the minimum required value. Return code 1 is returned if error 2015 is recoverable.
7. Error 2015 is recoverable or naux2<>0, and naux2 is too small--that is, less than the minimum required value. Return code 1 is returned if error 2015 is recoverable.

Example 1

This example shows how to compute a convolution of a sequence in H, where H and X are ramp functions. It calculates all nonzero values of the convolution of the sequences in H and X. The arrays are declared as follows:

     REAL*4   H(8), X(10,1), Y(17)

Because this convolution is symmetric in H and X, you can interchange the H and X sequences, leaving all other arguments the same, and you get the same output shown below. First, initialize AUX1 using the calling sequence shown below with INIT <> 0. Then use the same calling sequence with INIT = 0 to do the calculation.

Call Statement and Input

           INIT  H INC1H X INC1X INC2X Y INC1Y INC2Y NH  NX  M IY0 NY  AUX1 NAUX1 AUX2 NAUX2
            |    |   |   |   |     |   |   |     |    |   |  |  |   |   |     |    |     |
CALL SCONF(INIT, H , 1 , X , 1  ,  1 , Y,  1  ,  1  , 8, 10, 1, 0, 17, AUX1, 128, AUX2, 23)

Output

Y        =  (11.0, 34.0, 70.0, 120.0, 185.0, 266.0, 364.0, 480.0,
             516.0, 552.0, 567.0, 560.0, 530.0, 476.0, 397.0, 292.0,
             160.0)

Example 2

This example shows how the output from Example 1 differs when the value for NY is 21 rather than 17, and the value for IY0 is -2 rather than 0. This yields two zeros on each end of the convolution.

Output

Y        =  (0.0, 0.0, 11.0, 34.0, 70.0, 120.0, 185.0, 266.0, 364.0,
             480.0, 516.0, 552.0, 567.0, 560.0, 530.0, 476.0, 397.0,
             292.0, 160.0, 0.0, 0.0)

Example 3

This example shows how to compute the autoconvolution by letting the two input sequences be the same for Example 2. First, initialize AUX1 using the calling sequence shown below with INIT <> 0. Then use the same calling sequence with INIT = 0 to do the calculation.

Call Statement and Input

           INIT  H INC1H X INC1X INC2X Y INC1Y INC2Y NH  NX  M  IY0  NY  AUX1 NAUX1 AUX2 NAUX2
            |    |   |   |   |     |   |   |     |    |   |  |   |    |   |     |    |     |
CALL SCONF(INIT, H , 1 , H , 1  ,  1 , Y,  1  ,  1  , 8, 10, 1, -2, 21, AUX1, 128, AUX2, 23)

Output

Y        =  (1.0, 4.0, 10.0, 20.0, 35.0, 56.0, 84.0, 120.0, 147.0,
             164.0, 170.0, 164.0, 145.0, 112.0, 64.0)

Example 4

This example shows how to compute all nonzero values of the convolution of the sequence in H with the two sequences in X. First, initialize AUX1 using the calling sequence shown below with INIT <> 0. Then use the same calling sequence with INIT = 0 to do the calculation.

Call Statement and Input

           INIT  H INC1H X INC1X INC2X Y INC1Y INC2Y NH  NX  M IY0 NY  AUX1 NAUX1 AUX2 NAUX2
            |    |   |   |   |     |   |   |     |    |   |  |  |   |   |     |    |     |
CALL SCONF(INIT, H , 1 , X,  1  , 10 , Y,  1  , 17  , 8, 10, 2, 0, 17, AUX1, 148, AUX2, 43)

X contains the following two sequences:

11.0  12.0
12.0  13.0
13.0  14.0
14.0  15.0
15.0  16.0
16.0  17.0
17.0  18.0
18.0  19.0
19.0  20.0
20.0  11.0

Output

Y contains the following two sequences:

 11.0   12.0
 34.0   37.0
 70.0   76.0
120.0  130.0
185.0  200.0
266.0  287.0
364.0  392.0
480.0  516.0
516.0  552.0
552.0  578.0
567.0  582.0
560.0  563.0
530.0  520.0
476.0  452.0
397.0  358.0
292.0  237.0
160.0   88.0

Example 5

This example shows how to compute a correlation of a sequence in H, where H and X are ramp functions. It calculates all nonzero values of the correlation of the sequences in H and X. The arrays are declared as follows:

     REAL*4   H(8), X(10,1)

First, initialize AUX1 using the calling sequence shown below with INIT <> 0. Then use the same calling sequence with INIT = 0 to do the calculation.

Call Statement and Input

           INIT  H INC1H X INC1X INC2X Y INC1Y INC2Y NH  NX  M  IY0 NY  AUX1 NAUX1 AUX2 NAUX2
            |    |   |   |   |     |   |   |     |    |   |  |   |   |   |     |    |     |
CALL SCORF(INIT, H , 1 , X,  1  ,  1 , Y,  1  ,  1  , 8, 10, 1, -7, 17, AUX1, 128, AUX2, 23)

Output

Y        =  (88.0, 173.0, 254.0, 330.0, 400.0, 463.0, 518.0, 564.0,
             600.0, 636.0, 504.0, 385.0, 280.0, 190.0, 116.0,
             59.0, 20.0)

Example 6

This example shows how the output from Example 5 differs when the value for NY is 21 rather than 17, and the value for IY0 is -9 rather than 0. This yields two zeros on each end of the correlation.

Output

Y        =  (0.0, 0.0, 88.0, 173.0, 254.0, 330.0, 400.0, 463.0, 518.0,
             564.0, 600.0, 636.0, 504.0, 385.0, 280.0, 190.0, 116.0,
             59.0, 20.0, 0.0, 0.0)

Example 7

This example shows the effect of interchanging H and X. It uses the same input as Example 5, with H and X switched in the calling sequence, and with IY0 with a value of -9. Unlike convolution, as noted in Example 1, the correlation is not symmetric in H and X. First, initialize AUX1 using the calling sequence shown below with INIT <> 0. Then use the same calling sequence with INIT = 0 to do the calculation.

Call Statement and Input

           INIT  H INC1H X INC1X INC2X Y INC1Y INC2Y NH  NX  M  IY0 NY  AUX1 NAUX1 AUX2 NAUX2
            |    |   |   |   |     |   |   |     |    |   |  |   |   |   |     |    |     |
CALL SCONF(INIT, X , 1 , H,  1  ,  1 , Y,  1  ,  1  , 8, 10, 1, -9, 17, AUX1, 128, AUX2, 23)

Output

Y        =  (20.0, 59.0, 116.0, 190.0, 280.0, 385.0, 504.0, 636.0,
             600.0, 564.0, 518.0, 463.0, 400.0, 330.0, 254.0, 173.0,
             88.0)

Example 8

This example shows how to compute the autocorrelation by letting the two input sequences be the same. First, initialize AUX1 using the calling sequence shown below with INIT <> 0. Then use the same calling sequence with INIT = 0 to do the calculation. Because there is only one H input sequence, only one autocorrelation can be computed. Furthermore, this usage does not take advantage of the fact that the output is symmetric. Therefore, you should use SACORF to compute autocorrelations, because it does not have either of these problems.

Call Statement and Input

           INIT  H INC1H X INC1X INC2X Y INC1Y INC2Y NH NX M  IY0 NY  AUX1 NAUX1 AUX2 NAUX2
            |    |   |   |   |     |   |   |     |   |  |  |   |   |   |     |    |     |
CALL SCONF(INIT, H , 1 , H,  1  ,  1 , Y,  1  ,  1 , 8, 8, 1, -7, 15, AUX1, 148, AUX2, 43)

Output

Y        =  (8.0, 23.0, 44.0, 70.0, 100.0, 133.0, 168.0, 204.0, 168.0,
             133.0, 100.0 , 70.0, 44.0, 23.0, 8.0)

Example 9

This example shows how to compute all nonzero values of the correlation of the sequence in H with the two sequences in X. First, initialize AUX1 using the calling sequence shown below with INIT <> 0. Then use the same calling sequence with INIT = 0 to do the calculation.

Call Statement and Input

           INIT  H INC1H X INC1X INC2X Y INC1Y INC2Y NH  NX  M  IY0 NY  AUX1 NAUX1 AUX2 NAUX2
            |    |   |   |   |     |   |   |     |    |   |  |   |   |   |     |    |     |
CALL SCONF(INIT, H , 1 , X,  1  , 10 , Y,  1  , 17  , 8, 10, 2, -7, 17, AUX1, 148, AUX2, 43)

Output

Y contains the following two sequences:

 88.0   96.0
173.0  188.0
254.0  275.0
330.0  356.0
400.0  430.0
463.0  496.0
518.0  553.0
564.0  600.0
600.0  636.0
636.0  592.0
504.0  462.0
385.0  346.0
280.0  245.0
190.0  160.0
116.0   92.0
 59.0   42.0
 20.0   11.0