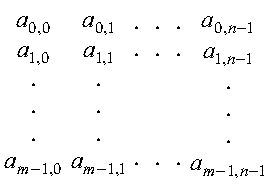

A sequence is an ordered collection of numbers. It can be a one-, two-, or three-dimensional sequence. Sequences are used in the areas of sorting, searching, Fourier transforms, convolutions, and correlations.
Sequences can contain either real or complex data. For sequences containing complex data, a special storage arrangement is used to accommodate the two parts, a and b, of each complex number, a+bi, in the array. For each complex number, two sequential storage locations are required in the array. Therefore, exactly twice as much storage is required for complex sequences as for real sequences of the same precision. See How Do You Set Up Your Scalar Data? for a description of real and complex numbers, and How Do You Set Up Your Arrays? for a description of how real and complex data is stored in arrays.
A one-dimensional sequence appears symbolically as follows, where the subscripts indicate the element positions within the sequence:
A one-dimensional sequence is stored in an array using stride in the same way a vector uses stride. For details, see How Stride Is Used for Vectors.
A two-dimensional sequence appears symbolically as a series of columns of elements. (They are represented in the same way as a matrix without the square brackets.) The two subscripts indicate the element positions in the first and second dimensions, respectively:
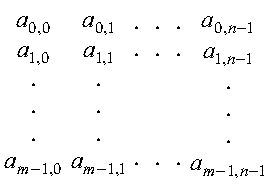
A two-dimensional sequence is stored in an array using the stride for the second dimension in the same way that a matrix uses leading dimension. It uses a stride of 1 for the first dimension. For details, see How Leading Dimension Is Used for Matrices. (In the area of Fourier transforms, a two-dimensional sequence may be stored in transposed form in an array. In this case, the stride for the second dimension is 1, and the stride for the first dimension is the leading dimension of the array.)
A three-dimensional sequence is represented as a series of blocks of elements. Each block is equivalent to a two-dimensional sequence. The number of blocks indicates the length of the third dimension. The three subscripts indicate the element positions in the first, second, and third dimensions, respectively:
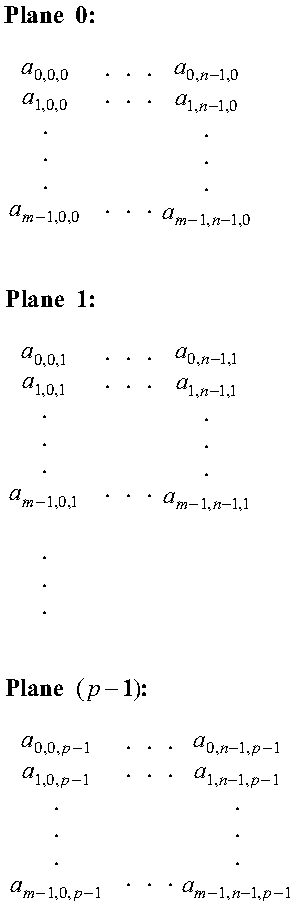
Each block of elements in a three-dimensional sequence is stored successively in an array. The stride for the third dimension is used to select the elements for each successive block of elements in the array. The starting point of the three-dimensional sequence is specified as the argument for the sequence in the ESSL calling statement. For example, if the three-dimensional sequence is contained in array BIG, declared as BIG(1:20,1:30,1:10), and starts at the second element in the first dimension, the third element in the second dimension, and the first element in the third dimension of array BIG, you should specify BIG(2,3,1) as the argument for the sequence, such as in:
CALL SCFT3 (BIG(2,3,1),20,600,Y,32,2056,16,20,10,1,1.0,AUX,30000)
See How Stride Is Used for Three-Dimensional Sequences for a detailed description of how three-dimensional sequences are stored within arrays using strides.
The elements of the three-dimensional sequence can be defined as aijk for i = 1, m, j = 1, n, and k = 1, p. The first two subscripts, i and j, define the elements in the first two dimensions of the sequence, and the third subscript, k, defines the elements in the third dimension. Using this definition of three-dimensional sequences, this section explains how these elements are mapped into an array using the concepts of stride. (Remember that the elements aijk are the elements of the conceptual data structure, the three-dimensional sequence to be processed by ESSL. The sequence does not have to include all the elements in the array. Strides are used by the ESSL subroutines to select the desired elements to be processed in the array.)
The sequence elements in the first two dimensions are mapped into an array in the same way a matrix or two-dimensional sequence is mapped into an array. It uses all the items listed in How Leading Dimension Is Used for Matrices, such as the starting point, the number of rows and columns, and the leading dimension. The stride for the first dimension, inc1, of a three-dimensional sequence is assumed to be 1, as for matrices. The stride for the second dimension, inc2, of a three-dimensional sequence is equivalent to the leading dimension for a matrix.
The stride for the third dimension, inc3, is used to define the array elements that make up the third dimension of the three-dimensional sequence. The stride for the third dimension is used as an increment to step through the array to find the starting point for each of the p successive blocks of elements in the array. The stride, inc3, must always be positive. It must always be greater than or equal to the number of elements to be processed in the first two dimensions; that is, inc3 >= (inc2)(n).
A three-dimensional sequence is usually stored in a one-, two-, or three-dimensional array; however, for the sake of this discussion, a three-dimensional array is used here. For an array, A, declared as A(E1:E2,F1:F2,G1:G2), the strides in the first, second, and third dimensions are:
Given an array A, declared as A(1:7,1:3,0:3), where the lengths of the first, second, and third dimensions are 7, 3, and 4, respectively, the resulting strides are inc1 = 1, inc2 = 7, and inc3 = 21.
The starting point for a three-dimensional sequence in an array is at the location specified by the argument for the sequence in the ESSL calling statement. Using the array A, described above, if you specify A(2,2,1) for a three-dimensional sequence, where A is defined as follows, in four blocks, for planes 0 - 3, respectively:
1.0 8.0 15.0 22.0 29.0 36.0 43.0 50.0 57.0 64.0 71.0 78.0 2.0 9.0 16.0 23.0 30.0 37.0 44.0 51.0 58.0 65.0 72.0 79.0 3.0 10.0 17.0 24.0 31.0 38.0 45.0 52.0 59.0 66.0 73.0 80.0 4.0 11.0 18.0 25.0 32.0 39.0 46.0 53.0 60.0 67.0 74.0 81.0 5.0 12.0 19.0 26.0 33.0 40.0 47.0 54.0 61.0 68.0 75.0 82.0 6.0 13.0 20.0 27.0 34.0 41.0 48.0 55.0 62.0 69.0 76.0 83.0 7.0 14.0 21.0 28.0 35.0 42.0 49.0 56.0 63.0 70.0 77.0 84.0
then processing begins in the second block of elements at row 2 and column 2 in array A, which is 30.0. The stride in the third dimension is then used to find the starting point for each of the next p-1 successive blocks of elements in the array. The stride, inc3, is added to the starting point p-1 times. In this example, the stride for the third dimension is 21, and the number of blocks of elements, p, to be processed is 3, so the starting points in array A are A(2,2,1), A(2,2,2), and A(2,2,3). These are elements 30.0, 51.0, and 72.0. These array elements then correspond to the sequence elements a111, a112, and a113, respectively.
In general terms, this results in the following starting positions for the blocks of elements in the array:
Using m = 4, n = 2, and
p = 3 to define the elements of the three-dimensional data
structure in this example, the resulting three-dimensional sequence is defined
as follows, in three blocks, for planes 0 - 2, respectively:
|
| Plane 0: | Plane 1: | Plane 2: | |||
| a000 | a010 | a001 | a011 | a002 | a012 |
| a100 | a110 | a101 | a111 | a102 | a112 |
| a200 | a210 | a201 | a211 | a202 | a212 |
| a300 | a310 | a301 | a311 | a302 | a312 |
| Plane 0: | Plane 1: | Plane 2: | |||
| 30.0 | 37.0 | 51.0 | 58.0 | 72.0 | 79.0 |
| 31.0 | 38.0 | 52.0 | 59.0 | 73.0 | 80.0 |
| 32.0 | 39.0 | 53.0 | 60.0 | 74.0 | 81.0 |
| 33.0 | 40.0 | 54.0 | 61.0 | 75.0 | 82.0 |
As shown in this example, the three-dimensional sequence does not have to include all the blocks of elements in the array. In this case, the three-dimensional sequence includes only the second through the fourth block of elements in the array. The first block is not used. Elements of an array are selected as they are arranged in storage, regardless of the number of dimensions defined in the array. Therefore, when using a one- or two-dimensional array to store your three-dimensional sequence, you should understand how your array elements are stored to ensure that elements are selected properly. See Setting Up Arrays in Fortran for a description of array storage.