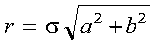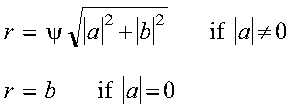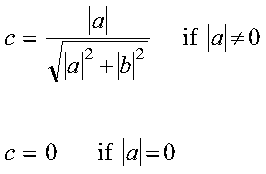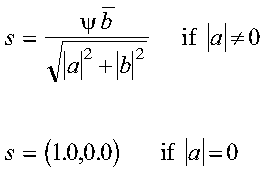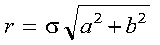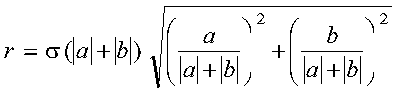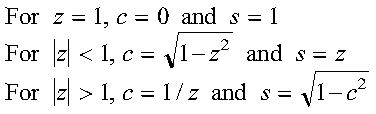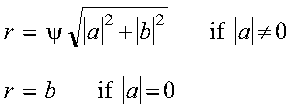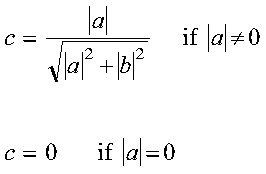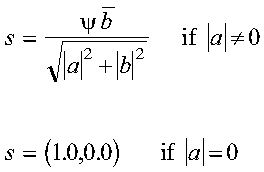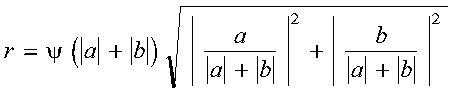Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SROTG, DROTG, CROTG, and ZROTG--Construct a Givens Plane Rotation

SROTG and DROTG construct a real Givens plane rotation, and CROTG and ZROTG construct a complex Givens plane rotation. The computations use rotational elimination parameters a and b. Values are returned for r, as well as the cosine c and the sine s of the angle of rotation. SROTG and DROTG also return a value for z.

Note:

Throughout this description, the symbols r and z are used to represent two of the output values returned for this computation. It is important to note that the values for r and z are actually returned in the input-output arguments a and b, respectively, overwriting the original values passed in a and b.

Table 48. Data Types

Syntax

On Entry

a

is the rotational elimination parameter a. Specified as: a number of the data type indicated in Table 48.

b

is the rotational elimination parameter b. Specified as: a number of the data type indicated in Table 48.

c

See On Return.

s

See On Return.

On Return

a

is the value computed for r.

For SROTG and DROTG:

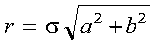
where:

sigma = SIGN(a) if |a| > |b|

sigma = SIGN(b) if |a| <= |b|

For CROTG and ZROTG:

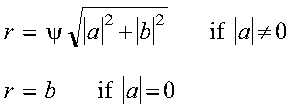
where:

psi = a/|a|

Returned as: a number of the data type indicated in Table 48.

b

is the value computed for z.

For SROTG and DROTG:

z = s    if |a| > |b|

z = 1/c    if |a| <= |b| and c <> 0 and r <> 0

z = 1    if |a| <= |b| and c = 0 and r <> 0

z = 0    if r = 0

For CROTG and ZROTG: no value is returned, and the input value is not changed.

Returned as: a number of the data type indicated in Table 48.

c

is the cosine c of the angle of (Givens) rotation. For SROTG and DROTG:

c = a/r    if r <> 0

c = 1    if r = 0

For CROTG and ZROTG:

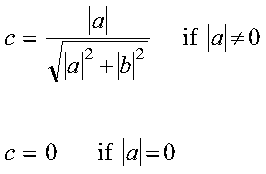
Returned as: a number of the data type indicated in Table 48.

s

is the sine s of the angle of (Givens) rotation.

For SROTG and DROTG:

s = b/r    if r <> 0

s = 0    if r = 0

For CROTG and ZROTG:

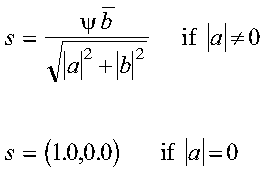
where psi = a/|a|

Returned as: a number of the data type indicated in Table 48.

Note

In your C program, arguments a, b, c, and s must be passed by reference.

Function

SROTG and DROTG

A real Givens plane rotation is constructed for values a and b by computing values for r, c, s, and z, where:

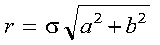
where:

sigma = SIGN(a)    if |a| > |b|

sigma = SIGN(b)    if |a| <= |b|

c = a/r    if r <> 0

c = 1    if r = 0

s = b/r    if r <> 0

s = 0    if r = 0

z = s    if |a| > |b|

z = 1/c    if |a| <= |b| and c <> 0 and r <> 0

z = 1    if |a| <= |b| and c = 0 and r <> 0

z = 0    if r = 0

See reference [79].

Following are some important points about the computation:

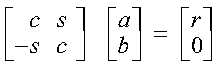
1. The numbers for c, s, and r satisfy:

   
   
   

   
   
2. Where necessary, scaling is used to avoid overflow and destructive underflow in the computation of r, which is expressed as follows:

   
   
   
   

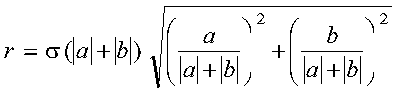
3. sigma is not essential to the computation of a Givens rotation matrix, but its use permits later stable reconstruction of c and s from just one stored number, z. See reference [91]. c and s are reconstructed from z as follows:

   
   
   
   

CROTG and ZROTG

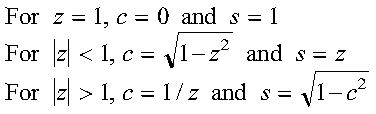
A complex Givens plane rotation is constructed for values a and b by computing values for r, c, and s, where:

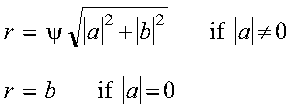
where:

psi = a/|a|

See reference [79].

Following are some important points about the computation:

1. The numbers for c, s, and r satisfy:

   
   
   

   
   
2. Where necessary, scaling is used to avoid overflow and destructive underflow in the computation of r, which is expressed as follows:

   
   
   
   

Error Conditions

Computational Errors

None

Input-Argument Errors

None

Example 1

This example shows the construction of a real Givens plane rotation, where r is 0.

Call Statement and Input

             A     B    C   S
             |     |    |   |
CALL SROTG( 0.0 , 0.0 , C , S )

Output

A        =  0.0
B        =  0.0
C        =  1.0
S        =  0.0

Example 2

This example shows the construction of a real Givens plane rotation, where c is 0.

Call Statement and Input

             A     B    C   S
             |     |    |   |
CALL SROTG( 0.0 , 2.0 , C , S )

Output

A        =  2.0
B        =  1.0
C        =  0.0
S        =  1.0

Example 3

This example shows the construction of a real Givens plane rotation, where |b| > |a|.

Call Statement and Input

             A      B    C   S
             |      |    |   |
CALL SROTG( 6.0 , -8.0 , C , S )

Output

A        =  -10.0
                 _
B        =  -1.666
C        =  -0.6
S        =  0.8

Example 4

This example shows the construction of a real Givens plane rotation, where |a| > |b|.

Call Statement and Input

             A     B    C   S
             |     |    |   |
CALL SROTG( 8.0 , 6.0 , C , S )

Output

A        =  10.0
B        =  0.6
C        =  0.8
S        =  0.6

Example 5

This example shows the construction of a complex Givens plane rotation, where |a| = 0.

Call Statement and Input

            A   B   C   S
            |   |   |   |
CALL CROTG( A , B , C , S )
 
A        =  (0.0, 0.0)
B        =  (1.0, 0.0)
 

Output

A        =  (1.0, 0.0)
C        =  0.0
S        =  (1.0, 0.0)

Example 6

This example shows the construction of a complex Givens plane rotation, where |a| <> 0.

Call Statement and Input

            A   B   C   S
            |   |   |   |
CALL CROTG( A , B , C , S )
 
A        =  (3.0, 4.0)
B        =  (4.0, 6.0)

Output

A        =  (5.26, 7.02)
C        =  0.57
S        =  (0.82, -0.05)