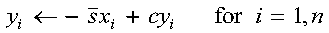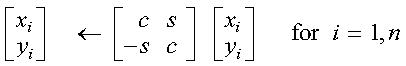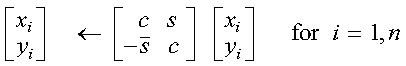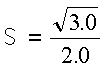Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference
SROT and DROT apply a real plane rotation to real vectors; CROT and
ZROT apply a complex plane rotation to complex vectors; and CSROT and
ZDROT apply a real plane rotation to complex vectors. The plane
rotation is applied to n points, where the points to be rotated are
contained in vectors x and y, and where the cosine and
sine of the angle of rotation are c and s,
respectively.
Table 49. Data Types
| x, y
| c
| s
| Subprogram
|
| Short-precision real
| Short-precision real
| Short-precision real
| SROT
|
| Long-precision real
| Long-precision real
| Long-precision real
| DROT
|
| Short-precision complex
| Short-precision real
| Short-precision complex
| CROT
|
| Long-precision complex
| Long-precision real
| Long-precision complex
| ZROT
|
| Short-precision complex
| Short-precision real
| Short-precision real
| CSROT
|
| Long-precision complex
| Long-precision real
| Long-precision real
| ZDROT
|
| Fortran
| CALL SROT | DROT | CROT | ZROT | CSROT | ZDROT (n, x,
incx, y, incy, c, s)
|
| C and C++
| srot | drot | crot | zrot | csrot | zdrot (n, x,
incx, y, incy, c, s);
|
| PL/I
| CALL SROT | DROT | CROT | ZROT | CSROT | ZDROT (n, x,
incx, y, incy, c, s);
|
- n
- is the number of points to be rotated--that is, the number of
elements in vectors x and y. Specified as:
a fullword integer; n >= 0.
- x
- is the vector x of length n, containing the
xi coordinates of the points to be
rotated. Specified as: a one-dimensional array of (at least)
length 1+(n-1)|incx|, containing numbers of the data
type indicated in Table 49.
- incx
- is the stride for vector x. Specified as: a
fullword integer. It can have any value.
- y
- is the vector y of length n, containing the
yi coordinates of the points to be
rotated. Specified as: a one-dimensional array of (at least)
length 1+(n-1)|incy|, containing numbers of the data
type indicated in Table 49.
- incy
- is the stride for vector y. Specified as: a
fullword integer. It can have any value.
- c
- the cosine, c, of the angle of rotation. Specified
as: a number of the data type indicated in Table 49.
- s
- the sine, s, of the angle of rotation. Specified as:
a number of the data type indicated in Table 49.
- x
- is the vector x of length n, containing the rotated
xi coordinates, where:
- xi <--
cxi+syi
for i = 1,
Returned as: a one-dimensional array, containing numbers of the data
type indicated in Table 49.
- y
- is the vector y of length n, containing the rotated
yi coordinates, where:
For SROT, DROT, CSROT, and ZDROT:
- yi <--
-sxi+cyi
for i = 1, n
For CROT and ZROT:
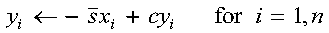
Returned as: a one-dimensional array, containing numbers of the data
type indicated in Table 49.
The vectors x and y must have no common
elements; otherwise, results are unpredictable. See Concepts.
Applying a plane rotation to n points, where the points to be
rotated are contained in vectors x and y, is expressed
as follows, where c and s are the cosine and sine of the
angle of rotation, respectively. For SROT, DROT, CSROT, and
ZDROT:
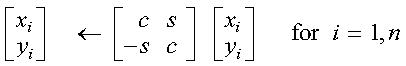
For CROT and ZROT:
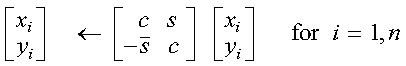
See references [57] and [79]. No computation is
performed if n is 0 or if c is 1.0 and s is
zero. For SROT, CROT, and CSROT, intermediate results are accumulated
in long precision.
None
n < 0
This example shows how to apply a real plane rotation to real vectors
x and y having positive strides.
N X INCX Y INCY C S
| | | | | | |
CALL SROT( 5 , X , 1 , Y , 2 , 0.5 , S )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (-1.0, . , -2.0, . , -3.0, . , -4.0, . , -5.0)
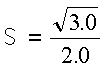
X = (-0.366, -0.732, -1.098, -1.464, -1.830)
Y = (-1.366, -2.732, -4.098, -5.464, -6.830)
This example shows how to apply a real plane rotation to real vectors
x and y having strides of opposite sign.
N X INCX Y INCY C S
| | | | | | |
CALL SROT( 5 , X , 1 , Y , -1 , 0.5 , S )
X = (1.0, 2.0, 3.0, 4.0, 5.0)
Y = (-5.0, -4.0, -3.0, -2.0, -1.0)
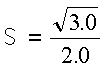
X =(same as output X in Example 1)
Y = (-6.830, -5.464, -4.098, -2.732, -1.366)
This example shows how scalar values in vectors x and
y can be processed by specifying 0 strides and the number of
elements to be processed, n, equal to 1.
N X INCX Y INCY C S
| | | | | | |
CALL SROT( 1 , X , 0 , Y , 0 , 0.5 , S )
X = (1.0)
Y = (-1.0)
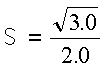
X = (-0.366)
Y = (-1.366)
This example shows how to apply a complex plane rotation to complex vectors
x and y having positive strides.
N X INCX Y INCY C S
| | | | | | |
CALL CROT( 3 , X , 1 , Y , 2 , 0.5 , S )
X = ((1.0, 2.0), (2.0, 3.0), (3.0, 4.0))
Y = ((-1.0, 5.0), . , (-2.0, 4.0), . , (-3.0, 3.0))
S = (0.75, 0.50)
X = ((-2.750, 4.250), (-2.500, 3.500), (-2.250, 2.750))
Y = ((-2.250, 1.500), . , (-4.000, 0.750), . ,
(-5.750, 0.000))
This example shows how to apply a real plane rotation to complex vectors
x and y having positive strides.
N X INCX Y INCY C S
| | | | | | |
CALL CSROT( 3 , X , 1 , Y , 2 , 0.5 , S )
X = ((1.0, 2.0), (2.0, 3.0), (3.0, 4.0))
Y = ((-1.0, 5.0), . , (-2.0, 4.0), . , (-3.0, 3.0))
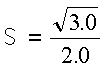
X = ((-0.366, 5.330), (-0.732, 4.964), (-1.098, 4.598))
Y = ((-1.366, 0.768), . , (-2.732, -0.598), . ,
(-4.098, -1.964))
[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]