Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SSCAL, DSCAL, CSCAL, ZSCAL, CSSCAL, and ZDSCAL--Multiply a Vector X by a Scalar and Store in the Vector X

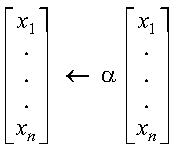
These subprograms perform the following computation, using the scalar alpha and the vector x:

x<--alphax

Table 50. Data Types

Syntax

On Entry

n

is the number of elements in vector x. Specified as: a fullword integer; n >= 0.

alpha

is the scalar alpha. Specified as: a number of the data type indicated in Table 50.

x

is the vector x of length n. Specified as: a one-dimensional array of (at least) length 1+(n-1)|incx|, containing numbers of the data type indicated in Table 50.

incx

is the stride for vector x. Specified as: a fullword integer. It can have any value.

On Return

x

is the vector x of length n, containing the result of the computation alphax. Returned as: a one-dimensional array, containing numbers of the data type indicated in Table 50.

Note

The fastest way in ESSL to zero out contiguous (stride 1) arrays is to call SSCAL or DSCAL, specifying incx = 1 and alpha = 0.

Function

The computation is expressed as follows:

See reference [79]. If n is 0, no computation is performed. For CSCAL, intermediate results are accumulated in long precision.

Error Conditions

Computational Errors

None

Input-Argument Errors

n < 0

Example 1

This example shows a vector, x, with a stride of 1.

Call Statement and Input

            N  ALPHA  X  INCX
            |    |    |   |
CALL SSCAL( 5 , 2.0 , X , 1  )
 
X        =  (1.0, 2.0, 3.0, 4.0, 5.0)

Output

X        =  (2.0, 4.0, 6.0, 8.0, 10.0)

Example 2

This example shows vector, x, with a stride greater than 1.

Call Statement and Input

            N  ALPHA  X  INCX
            |    |    |   |
CALL SSCAL( 5 , 2.0 , X , 2  )
 
X        =  (1.0, . , 2.0, . , 3.0, . , 4.0, . , 5.0)

Output

X        =  (2.0, . , 4.0, . , 6.0, . , 8.0, . , 10.0)

Example 3

This example illustrates that when the strides for two similar computations (Example 1 and Example 3) have the same absolute value but have opposite signs, the output is the same. This example is the same as Example 1, except the stride for x is negative (-1). For performance reasons, it is better to specify the positive stride. For x, processing begins at element X(5), which is 5.0, and results are stored beginning at the same element.

Call Statement and Input

            N  ALPHA  X   INCX
            |    |    |    |
CALL SSCAL( 5 , 2.0 , X , -1  )
 
X        =  (1.0, 2.0, 3.0, 4.0, 5.0)

Output

X        =  (2.0, 4.0, 6.0, 8.0, 10.0)

Example 4

This example shows how SSCAL can be used to compute a scalar value. In this case, input vector x contains a scalar value, and the stride is 0. The number of elements to be processed, n, is 1.

Call Statement and Input

            N  ALPHA  X  INCX
            |    |    |   |
CALL SSCAL( 1 , 2.0 , X , 0  )
 
X        =  (1.0)

Output

X        =  (2.0)

Example 5

This example shows a scalar, alpha, and a vector, x, containing complex numbers, where vector x has a stride of 1.

Call Statement and Input

            N  ALPHA  X  INCX
            |    |    |   |
CALL CSCAL( 3 ,ALPHA, X , 1  )
 
ALPHA    =  (2.0, 3.0)
X        =  ((1.0, 2.0), (2.0, 0.0), (3.0, 5.0))

Output

X        =  ((-4.0, 7.0), (4.0, 6.0), (-9.0, 19.0))

Example 6

This example shows a scalar, alpha, containing a real number, and a vector, x, containing complex numbers, where vector x has a stride of 1.

Call Statement and Input

             N  ALPHA  X  INCX
             |    |    |   |
CALL CSSCAL( 3 , 2.0 , X , 1  )
 
X        =  ((1.0, 2.0), (2.0, 0.0), (3.0, 5.0))

Output

X        =  ((2.0, 4.0), (4.0, 0.0), (6.0, 10.0))