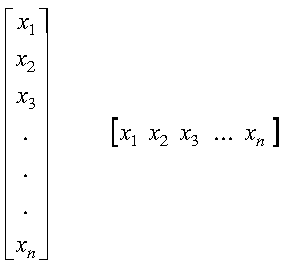

This section explains the special notations and conventions used in this book to describe various types of data.
Following are the special notations used in the examples in this book for
scalar data items. These notations are used to simplify the examples,
and they do not imply usage of any precision. For a definition of
scalar data in Fortran, C, C++, and PL/I, see Chapter 4, Coding Your Program.
| Data Item | Example | Description |
|---|---|---|
| Character item | 'T' | Character(s) in single quotation marks |
| Hexadecimal string | X'97FA00C1' | String of 4-bit hexadecimal characters |
| Logical item | .TRUE. .FALSE. | True or false logical value, as indicated |
| Integer data | 1 | Number with no decimal point |
| Real data | 1.6 | Number with a decimal point |
| Complex data | (1.0,-2.9) | Real part followed by the imaginary part |
|
|
_ 1.6666 |
|
A vector is represented as a single row or column of subscripted elements enclosed in square brackets. The subscripts refer to the element positions within the vector:
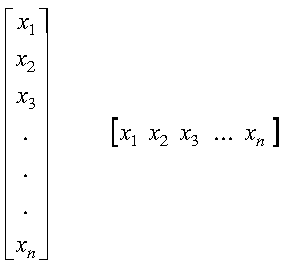
For a definition of vector, see Vectors.
A matrix is represented as a block of elements enclosed in square brackets. Subscripts refer to the row and column positions, respectively:
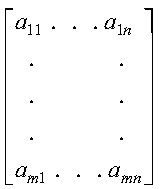
For a definition of matrix, see Matrices.
Sequences are used in the areas of sorting, searching, Fourier transforms, convolutions, and correlations. For a definition of sequences, see Sequences.
A one-dimensional sequence is represented as a series of elements enclosed in parentheses. Subscripts refer to the element position within the sequence:
A two-dimensional sequence is represented as a series of columns of elements. (They are represented in the same way as a matrix without the square brackets.) Subscripts refer to the element positions within the first and second dimensions, respectively:
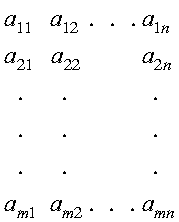
A three-dimensional sequence is represented as a series of blocks of elements. Subscripts refer to the elements positions within the first, second, and third dimensions, respectively:
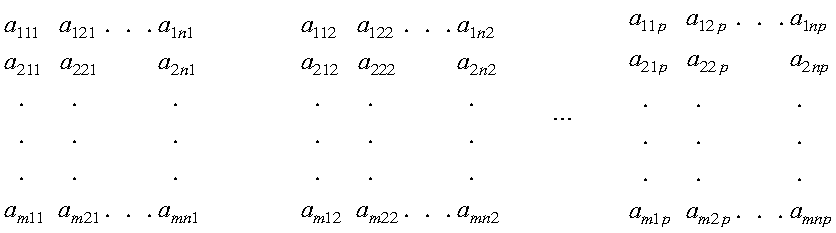
Arrays contain vectors, matrices, or sequences. For a definition of array, see How Do You Set Up Your Arrays?.
A one-dimensional array is represented as a single row of numeric elements enclosed in parentheses:
(1.0, 2.0, 3.0, 4.0, 5.0)
Elements not significant to the computation are usually not shown in the array. One dot appears for each element not shown. In the following array, five elements are significant to the computation, and two elements not used in the computation exist between each of the elements shown:
(1.0, . , . ,2.0, . , . ,3.0, . , . ,4.0, . , . ,5.0)
This notation is used to show vector elements inside an array.
A two-dimensional array is represented as a block of numeric elements enclosed in square brackets:
* *
| 1.0 11.0 5.0 25.0 |
| 2.0 12.0 6.0 26.0 |
| 3.0 13.0 7.0 27.0 |
| 4.0 14.0 8.0 28.0 |
* *
Elements not significant to the computation are usually not shown in the array. One dot appears for each element not shown. The following array contains three rows and two columns not used in the computation:
* *
| . . . . . . |
| . . . . . . |
| . 1.0 2.0 5.0 4.0 . |
| . 2.0 3.0 6.0 3.0 . |
| . 3.0 4.0 7.0 2.0 . |
| . 4.0 5.0 8.0 1.0 . |
| . . . . . . |
* *
This notation is used to show matrix elements inside an array.
A three-dimensional array is represented as a series of blocks of elements separated by ellipses. Each block appears like a two-dimensional array:
* * * * * * | 1.0 11.0 5.0 25.0 | | 10.0 111.0 15.0 125.0 | | 100.0 11.0 15.0 25.0 | | 2.0 12.0 6.0 26.0 | | 20.0 112.0 16.0 126.0 | ... | 200.0 12.0 16.0 26.0 | | 3.0 13.0 7.0 27.0 | | 30.0 113.0 17.0 127.0 | | 300.0 13.0 17.0 27.0 | | 4.0 14.0 8.0 28.0 | | 40.0 114.0 18.0 128.0 | | 400.0 14.0 18.0 28.0 | * * * * * *
Elements not significant to the computation are usually not shown in the array. One dot appears for each element not shown, just as for two-dimensional arrays.